Преобразование базиса и координат
Пусть в En задана {ei} и {ei} –пара взаимных базисов, а {ei¢} и {ei¢} некоторая другая пара взаимных базисов. Запишем формулы преобразования базисных векторов:
1°. Переход ei « ei¢: ei¢ =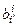 
ei; ei = 
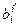ei¢. Здесь 
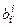– матрица перехода от ei к ei¢; 
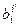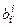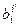– матрица перехода ei¢ от к ei; т.е.матрицы и взаимно-обратны: 
= 
.
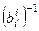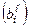2°.Переход ei « ei¢: ei¢ =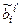 
ei; ei = 
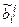ei¢. Здесь 
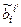– матрица перехода ei от к ei¢; 
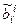– матрица перехода от ei к ei¢; т.е.матрицы 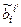и 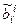взаимно-обратны.
T°. =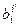 
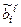и (следовательно 
= ).
◀ 
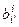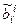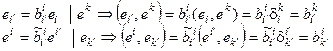.Положим k = i, k¢ = i¢ Þ 
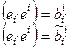, т.е. матрицы 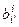и 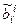совпадают ▶
Примечание: Правило нахождения матрицы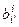
= 
.
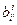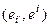Итак: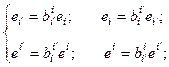 
– формулы преобразования базисных векторов. Здесь 
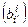матрица перехода от базиса {ei} к базису {ei¢}.
Таким образом для перехода от базиса {ei, ei} к базису {ei¢, ei¢} достаточно знать лишь матрицу перехода 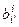от базиса {ei} к базису {ei¢}.
Задача. Имеется две пары взаимных базисов {e1, e2, e3, e1, e2, e3} и {e1, e2, e3, e1¢, e2¢, e3¢}. Записать формулы для преобразования при переходе от одного базиса к другому и найти соответствующие матрицы перехода.
◀ Формулы преобразования базисных векторов:
1) 
, 
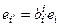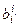– матрица перехода от ei к ei¢; i¢ – строки, i – столбцы(строки слева) 
.
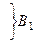2) 
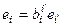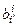, – матрица перехода от ei¢ к ei; i – строки, i¢ – столбцы (строки слева) 
,
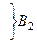при этом В2 = (В1)–1.
3) 
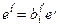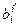, – матрица перехода от ei к ei¢; i¢– строки, i – столбцы (строки слева) 
,
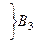при этом В3 = (В12)Т.
4) 
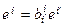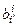, – матрица перехода от ei¢к ei; i – строки, i¢ – столбца (строки слева) 
,
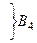при этом В4 = (В1)Т.
5) Элементы матрицы В1 = (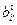 
) находят так 
▶
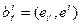Пример: Пусть е1(1, 1, 0) е1¢(1, 0, 0)
е2(1, 0, 1) е2¢(–1, 1, 0)
е3(0, 1, 1) е3¢(0, –1, 1)
Дата добавления: 2015-05-05; просмотров: 1572;