Примеры тензоров

1°. Нуль-тензор – это тензор все координаты которого, в некотором (а, следовательно, в

любом базисе) равны нулю.

2°. Символ Кронекера. Тензор А типа (1, 1) в базисе {e_i} имеет координаты .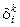

® = =

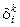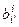
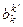
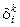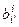
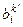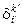
Т.е. 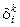действительно можно рассматривать как тензор типа (1, 1).

3°.Пусть А(x, y) – билинейная форма. Напомним, что в базисе {e_i}: A(x, y) = A(xⁱe_i, y^je_j) =

= A(e_i, e_j)xⁱy^j = a_ijxⁱy^j. Здесь a_ij – элементы матрицы билинейной формы А в базисе {e_i}.

Рассмотрим, как изменяется матрица билинейной формы при переходе к базису {e_i¢}.

a_ij = A(e_i¢, e_j¢) = 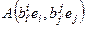= 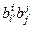A(e_i, e_j) = 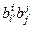a_ij.

Равенство a_ij = 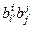a_ij, показывает, что матрица билинейной формы представляет собой тензор А типа (2, 0) ранга 2.

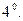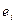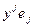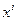
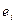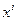Пусть А линейный оператор: y=Ax. В некотором базисе : =А( )= А =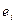

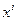
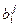
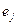
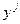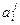
Т.е. = 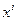, 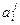– элементы матрицы линейного оператора в базисе {e_i¢}.

Рассмотрим базис { }.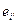

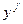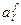
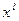= . Воспользуемся тем, что = ; = .

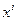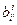
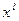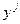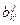
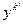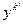
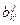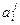
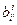
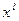= | умножим обе части на 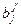и просуммируем по j.

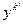
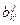
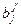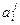
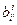
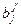
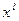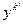
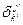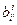
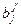
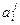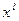= Þ =( ) Þ = .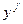

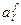
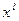Тогда =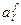

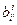
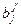
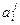
Последнее равенство показывает, что матрица линейного оператора может рассматриваться как тензор А типа (1,1) ранга 2.