Признак тензорности величины

Согласно определению, тензорный характер величины устанавливается по тому, как она преобразовывается при линейном ортогональном преобразовании координат.

Существует, однако, еще один способ установления тензорного характера величины. Проиллюстрируем этот способ на следующем примере:

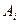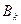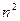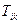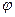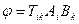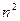Пусть и компоненты двух произвольных векторов. Если с помощью чисел можно образовать скаляр по правилу , то чисел 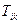образуют тензор 2-го ранга. Действительно:

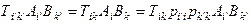
Вычитаем из левой части равенства правую:

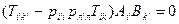
Отсюда, в силу произвольности векторов 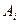и :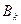

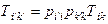
Т.е. числа 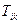действительно являются компонентами тензора второго ранга.

Аналогично формулируется и доказывается признак тензорности для тензора любого ранга.

Пользуясь признаком тензорности, легко проверить, что совокупность 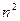чисел образующих символ Кронекера 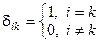является тензором 2-го ранга.

Действительно, возьмем произвольные векторы 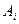и 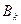и образуем выражение :

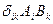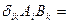
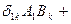
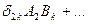
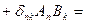
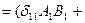
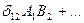
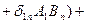
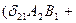
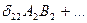
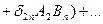
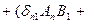
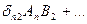
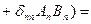
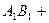
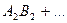
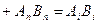- скаляр.

Следовательно, 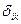тензор 2-го ранга. Он называется единичным тензором. Этот тензор обладает интересным свойством: он инвариантен относительно преобразования координат.

В самом деле: 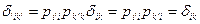- в силу ортогональности матрицы P.