Преобразование Лапласа (прямое и обратное) и его основные теоремы. Примеры.
Преобразования Лапласа играют очень важную роль при исследовании систем, описываемых дифференциальными уравнениями. С помощью прямого преобразования Лапласа можно перейти от дифференциальных уравнений к алгебраическим, решить их в алгебраической форме, а затем с помощью обратного преобразования получить искомый результат.
Прямое преобразование Лапласа осуществляется по формуле:
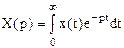 , (1)
, (1)
где 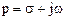 - комплексная переменная.
- комплексная переменная.
На функцию x(t) накладываются некоторые ограничения. Иногда для простоты пользуются символической записью выражения (1) в виде:
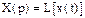 ,
,
где L - оператор прямого преобразования Лапласа.
Функция x(t) называется оригиналом, а Х(р) - изображением.
Кроме прямого существует также и обратное преобразование Лапласа, определяемое по формуле:
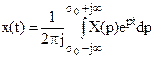 , (2)
, (2)
где интеграл берется на комплексной плоскости р вдоль любой прямой 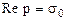 . Символически операцию обратного преобразования Лапласа по (2) записывают в виде:
. Символически операцию обратного преобразования Лапласа по (2) записывают в виде:
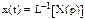 .
.
Обратное преобразование Лапласа можно определить по (2.2), из табл. 2.1, а также с помощью теоремы вычетов, из которой следует соотношение:
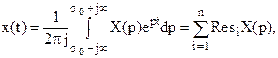
где Resi - вычеты подынтегральной функции 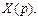
n - число полюсов функции 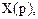 где она обращается в бесконечность.
где она обращается в бесконечность.
Вычет в простом полюсе определяется по формуле:
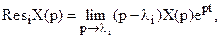
а вычет в полюсе кратности k:
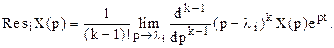
Укажем основные свойства преобразования Лапласа, широко используемые на практике.
1. Линейность оригиналов и изображений
Если у(t) = a1х1(t) + a2х2(t) + . . .,
то У(р) = а1Х1(р) + а2Х2(р) + . . . .
2. Дифференцирование оригинала
Если 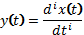 , то
, то 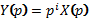 .
.
3. Интегрирование оригинала
Если 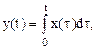 то
то 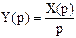 .
.
4. Задержка во времени оригинала
Если 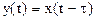 , то
, то 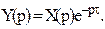
5. Свертка оригинала
Если 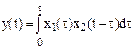 , то У(р) = Х1(р) Х2(р) .
, то У(р) = Х1(р) Х2(р) .
Это свойство гласит: свертке оригиналов соответствует произведение изображений.
6. Изменение масштаба времени оригинала
Если у(t) = x(at) , a>0, то 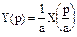 .
.
7. Смещение изображения
Если У(р) = Х(р+а) , то 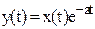 .
.
8. Умножение оригинала на время n раз
Если 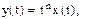 то
то 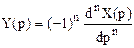 .
.
9. Деление оригинала на время
Если 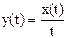 , то
, то 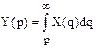 .
.
10. Предельное значение оригинала
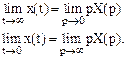
Дата добавления: 2015-06-17; просмотров: 8542;
