Основные виды регуляторов в аналоговых САУ.

Входной сигнал х в устройстве управления УУ преобразуется в сигнал u, который воздействует на объект управления ОУ. Функция преобразования сигнала х в сигнал u определяет тип регулятора в УУ.

1) Пропорциональный регулятор

Самым простым регулятором является пропорциональный регулятор, у которого сигнал u прямо пропорционален сигналу х, т.е. 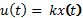, где k - коэффициент пропорциональности. Типичным пропорциональным регулятором является усилитель мощности.

2) Интегральный (интегрирующий) регулятор (интегратор)

В интегральном регуляторе или просто интеграторе сигнал u пропорционален интегралу по времени от сигнала х,

,

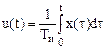где Т_и - постоянная времени интегратора.

Используется для отслеживания среднего значения.

3) Дифференциальный регулятор (дифференциатор)

В дифференциальном регуляторе или просто дифференциаторе сигнал пропорционален производной от сигнала х по времени:

,

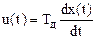где Т_д - постоянная времени дифференциатора.

Чем больше изменение, тем больше производная и тем большее воздействие на ОУ.

4) Пропорционально-интегральный регулятор

В пропорционально-интегральном регуляторе сигнал u пропорционален как сигналу х, так и интегралу по времени от него

.

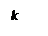
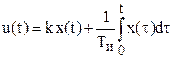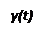
Рис.7 Структурная схема пропорционально-интегрирального регулятора

5) Пропорционально-дифференциальный регулятор

В пропорционально-дифференциальном регуляторе сигнал u пропорционален как сигналу х, так и производной по времени от него

.

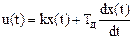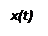
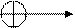Рис.8 Структурная схема пропорционально-дифференциального регулятора

6) Пропорционально-интегрально-дифференциальный регулятор

В пропорционально-интегрально-дифференциальном регуляторе сигнал u зависит от сигнала х, от интеграла его по времени и от производной его по времени

.

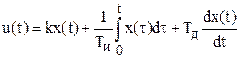Такие регуляторы применяются в системах, где надо отслеживать быстрые, умеренные и медленные изменения входного сигнала. На рис.9 приведена структурная схема такого регулятора.

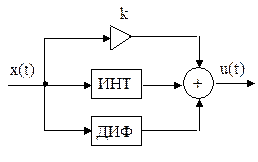
Рис.9 Структурная схема пропорционально-интегрально-дифференциального регулятора

Описание САУ с помощью дифференциальных уравнений. Классификация САУ по коэффициентам дифференциальных уравнений. Линеаризация САУ. Однородное дифференциальное уравнение и его решение.

Для анализа работы САУ необходимо иметь зависимости, связывающие входные и выходные сигналы звеньев. Эти зависимости определяются с помощью дифференциальных уравнений.

Связь между входным x(t) и выходным y(t) сигналами в САУ в общем случае описывается дифференциальным уравнением с постоянными коэффициентами вида:

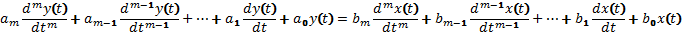
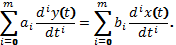
Введем символ дифференцирования 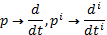. Тогда выражение 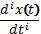можно записать в виде 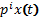. Запись вида 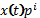в данном случае недопустима. Тогда ДУ с использованием символа дифференцирования можно записать в виде:

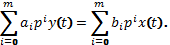
В этом выражении сигналы x(t) и y(t) нельзя выносить за знаки суммы, так как 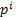не сомножители, а символы дифференцирования.

Классификация ДУ по коэффициентам 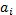и .

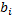1) Если коэффициенты в дифференциальном уравнении а_i и b_i не зависят от значений входного и выходного сигналов и их производных, то такие системы называются линейными.

2) Если хотя бы один из коэффициентов а_i, b_i зависит от значений сигналов х(t) и у(t) и их производных, то такие системы называются нелинейными.

3) Если хотя бы один из коэффициентов а_i, b_i зависит от времени, т.е. изменяется во времени, то такие системы называются параметрическими или стохастическими (второе имеет место при случайном характере изменений коэффициентов во времени).

4) Если коэффициенты а_i, b_i зависят от времени, а также от уровня сигналов х(t), y(t) и их производных, то такие системы называются нелинейно-параметрическими или нелинейно-стохастическими.

Строго говоря, все системы автоматического управления являются нелинейно-параметрическими. Исследование таких систем является очень сложной задачей. Однако в ряде случаев можно сделать ряд обоснованных допущений, позволяющих упростить исследование САУ. Одним из важнейших является допущение о том, что при малых значениях входного и выходного сигналов коэффициенты а_i и b_i можно считать постоянными, а саму систему линейной.

Линеаризация САУ.

При малых входных воздействиях любые САУ описываются приближенно линейным ДУ.

При прекращении входного воздействия САУ описывается однородным дифференциальным уравнением вида:

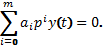
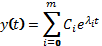
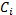– коэффициент, определенный при t = 0.

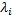– корни характеристического уравнения (полюсы).

Характеристическое уравнение – алгебраическое уравнение, которое получается из однородного ДУ заменой