Передаточная функция САУ. Определение и связь с дифференциальным уравнением САУ.

Передаточной функцией системы называется отношение изображения по Лапласу выходного сигнала к изображению по Лапласу входного сигнала:

.

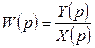Преобразование Лапласа этого сигнала есть функция комплексной переменной, задаваемая интегралом:

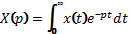
Сигнал называется оригиналом, а функция – его изображением по Лапласу (для краткости, просто изображением).

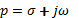– комплексная переменная.

С помощью прямого преобразования Лапласа можно перейти от дифференциальных уравнений к алгебраическим, решить их в алгебраической форме, а затем с помощью обратного преобразования получить искомый результат.

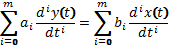
Для дифференциального уравнения используются первые две теоремы преобразования Лапласа:

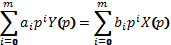
В этом выражении 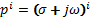являются сомножителями, поэтому изображения Y(p) и X(p) можно вынести за знаки сумм, в результате получим:

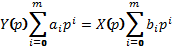
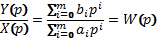
Это выражение показывает, что передаточная функция системы описывается дробно-рациональной функцией, являющейся отношением двух полиномов комплексного аргумента .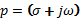

Это выражение устанавливает взаимно-однозначную связь передаточной функции САУ с ее дифференциальным уравнением. Отсюда следует, что по ДУ можно однозначно записать передаточную функцию, а по виду передаточной функции – ДУ системы. Любая САУ однозначно определяется коэффициентами 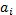и и 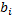порядком m ДУ.