Комплексный сигнал, комплексный коэффициент передачи (ККП), годограф ККП (на примере RC-звена).

Для исследования различных устройств и систем в качестве входного сигнала часто используют гармонические сигналы вида 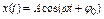, где A, 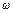, 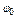- амплитуда, угловая частота и начальная фаза гармонического сигнала, 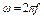, 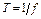- период гармонического сигнала.

Комплексный сигнал 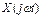получается из гармонического в результате следующего математического преобразования: = = .

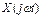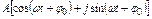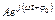Из этого выражения следует, что гармонический сигнал есть реальная часть от комплексного сигнала, т.е. .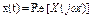

Комплексным коэффициентом передачи (ККП) устройства или системы называется отношение комплексного сигнала на выходе к комплексному сигналу на входе в установившемся режиме.

Под установившимся режимом понимается тот факт, что сигнал на входе действует бесконечно долго.

Математически это определение можно записать следующим образом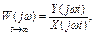

где 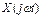, 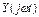- комплексные сигналы на входе и выходе.

Можно показать, что аналитическое выражение для ККП получается из выражения для передаточной функции W(p), в которой делается замена 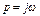, т.е.

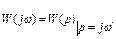
Тогда из 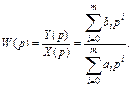получим: 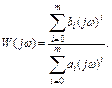(1)

Из этого выражения следует, что ККП является отношением полиномов аргумента .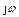

Выражения 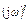при четных i дают действительные значения, а при нечетных - мнимые значения различных степеней частоты .

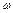Принимая это во внимание, выражение (1) для ККП перепишем в виде 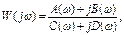(2)

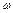где A( ), C( 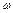) -полиномы с четными степенями частоты,

B( 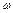), D( 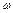) -полиномы с нечетными степенями частоты.

Помножим числитель и знаменатель (2) на выражение C( 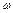) - jD( 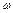). Избавимся таким образом от мнимости в знаменателе и получим

W(j 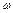) = P( 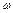) + jQ( 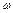), (3)

где P( 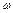) - действительная часть ККП, Q( 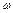) - мнимая часть ККП, причем ; .

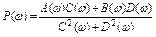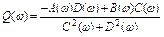Выражение (3) есть алгебраическая форма записи ККП. На практике ККП чаще представляется в показательной форме: 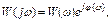(4) где 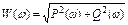- модуль ККП, 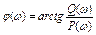- аргумент ККП.

Пример: 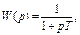тогда 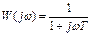= = 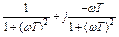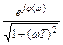,где .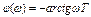

Если построить комплексную плоскость, ось абсцисс которой представляет действительные значения P( 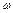), а ось ординат - мнимые значения 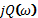комплексного коэффициента передачи, то при изменении частоты 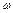от нуля до бесконечности на этой плоскости образуется последовательность точек - некая кривая, называемая годографом ККП.

На рис.10 приведен годограф ККП, описываемый выражением

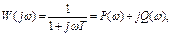где ; .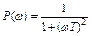

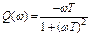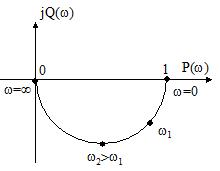
Рис.10 Годограф ККП инерционного устройства

При воздействии на вход линейной системы гармонического сигнала на ее выходе в установившемся режиме сигнал тоже будет гармоническим, причем частоты входного и выходного сигналов совпадают.

Выражение для выходного сигнала определяется по 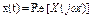с учетом :

,

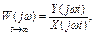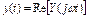где .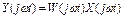

При перемножении комплексных чисел лучше всего использовать показательные формы их представления.

Тогда 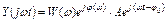= 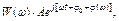откуда .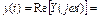

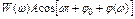Из этого выражения видно, что амплитуда выходного сигнала изменилась в W( 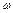) раз, а фаза получила приращение на величину .

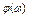9. Частотные характеристики САУ: АЧХ, ФЧХ, ЛАЧХ, ЛФЧХ (на примере RC-звена).

Амплитудно-частотной характеристикой (АЧХ) называется зависимость модуля ККП от частоты .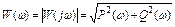

Фазочастотной характеристикой (ФЧХ) называется зависимость аргумента ККП от частоты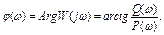

На рис.11 приведены АЧХ и ФЧХ инерционного устройства, ККП которого описывается выражением 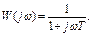Из него следует ,

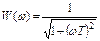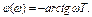
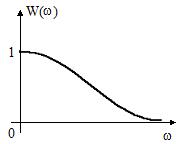
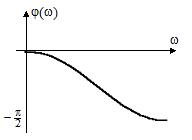
Рис.11 АЧХ и ФЧХ инерционного устройства