Импульсная характеристика

Другим широко используемым сигналом является единичный импульс, предложенный математиком Дираком. Он описывается выражением 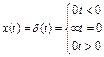, причем .

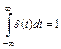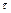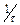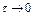Последнее условие свидетельствует о том, что площадь импульса Дирака равна единице. Единичный импульс есть предел прямоугольного импульса шириной и высотой при . Единичный импульс называют также дельта-функцией.

Имеет место замечательное фильтрующее во времени свойство единичного импульса .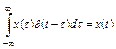

Это свойство гласит так: свертка любой функции с единичным импульсом равна значению функции в момент действия этого импульса.

Преобразование Лапласа от единичного импульса найдем, используя его фильтрующее свойство: .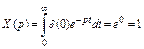

Импульсной характеристикой w(t) системы называется сигнал на ее выходе при воздействии на ее входе единичного импульса при нулевых начальных условиях.

Математически импульсная характеристика определяется по выражению, следующему из 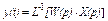с учетом :

.

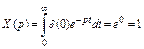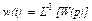Из этого выражения следует правило: импульсная характеристика системы есть обратное преобразование Лапласа от ее передаточной функции.

Для инерционного устройства 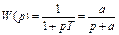, где .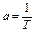

Тогда имеем: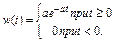

График этой импульсной характеристики приведен на рис.14:

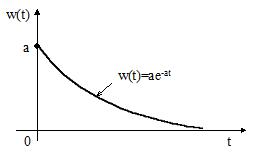
Рис.14 Импульсная характеристика инерционного устройства

Определим связь между импульсной и переходной характеристикой. Из 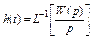следует, что прямое преобразование Лапласа от переходной характеристики:

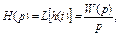откуда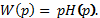

Возьмем обратное преобразование от левой и правой частей этого уравнения и получим

,

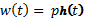где 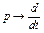- символ дифференцирования.

Таким образом, импульсная характеристика есть производная по времени от переходной характеристики.