Теорема 1.
Рис. 14
Дану аксіому легко перевірити експериментально і згідно з нею маємо, що умовами зрівноваження двох сил ( 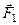 і
і 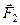 ), котрі діють на тверде тіло, є:
), котрі діють на тверде тіло, є:
а) спільність ліній їх дії;
б) виконання векторної рівності
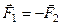 . (1.1)
. (1.1)
2. Аксіома приєднання і виключення зрівноваженої системи сил.
Стан твердого тіла не порушиться, якщо до системи сил, що діє на нього, приєднати або виключити систему зрівноважених сил.
Справедливість цього твердження випливає з визначення поняття “зрівноважена система сил” (див. § 4).
Наслідок.
Стан твердого тіла не порушиться при перенесенні точки прикладання сил вздовж лінії її дії в будь-яку точку тіла.
Наслідок не є аксіомою і його необхідно довести. Для доведення наслідку розглянемо тверде тіло, на яке в деякій точці  діє сила
діє сила  (рис. 15,а).
(рис. 15,а).
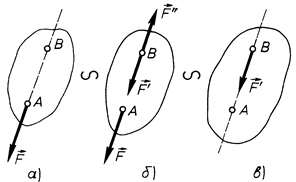
Рис. 15
Візьмемо на лінії дії сили  яку-небудь точку
яку-небудь точку  і прикладемо в цій точці дві сили
і прикладемо в цій точці дві сили 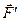 і
і 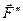 , які чисельно дорівнюють силі
, які чисельно дорівнюють силі  і задовольняють умові зрівноваження
і задовольняють умові зрівноваження 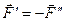 (рис. 15,б). Таке приєднання у відповідності до аксіоми 2 не порушує стану тіла, тобто система сил
(рис. 15,б). Таке приєднання у відповідності до аксіоми 2 не порушує стану тіла, тобто система сил 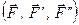 буде еквівалентна вихідній системі сил
буде еквівалентна вихідній системі сил 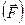 . Оскільки сили
. Оскільки сили 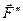 і
і  взаємно зрівноважуються (аксіома 1), їх, не порушуючи стану тіла, можна відкинути і одержимо одну силу
взаємно зрівноважуються (аксіома 1), їх, не порушуючи стану тіла, можна відкинути і одержимо одну силу 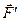 , яка прикладена в точці
, яка прикладена в точці  (рис. 15,в). Оскільки
(рис. 15,в). Оскільки 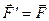 , то можна вважати, що сила
, то можна вважати, що сила 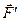 є силою
є силою  , яка перенесена вздовж лінії дії з точки
, яка перенесена вздовж лінії дії з точки  в точку
в точку  . Отже, наслідок доведений.
. Отже, наслідок доведений.
Доведене положення дає можливість, не порушуючи стану абсолютно твердого тіла, переносити сили, прикладені до нього, вздовж їх ліній дії в будь-які точки тіла.
Виходячи з класифікації векторів (вільний, невільний, ковзний), сила в статиці належить до ковзних векторів.
3. Аксіома дії і протидії (ІІІ-ій закон Ньютона).
Кожна механічна дія супроводжується рівною і про-тилежно напрямленою протидією.
Якщо дію позначити  , а протидію
, а протидію 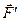 , то третя аксіома виражається такою векторною рівністю:
, то третя аксіома виражається такою векторною рівністю:
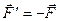 . (1.2)
. (1.2)
Оскільки дія і протидія прикладені до різних матеріальних об’єктів, то векторна рівність (1.2) не означає, що вони взаємно зрівноважені, адже аксіома і не вимагає, щоб сили були прикладені до одного і того ж тіла.
Треба відзначити також, що хоча третя аксіома говорить про механічну взаємодію, вона справедлива для більшості (а, можливо, і для всіх) взаємодій, які є в природі.
4. Аксіома накладання додаткових в’язей.
Рівновага матеріального об’єкта не порушиться при накладанні на нього додаткових в’язей.
Наприклад, рівновага парти (стола) не порушиться, якщо її ніжки прикріпити до підлоги болтами.
Частковим випадком даної аксіоми є твердження:
рівновага деформованого тіла не порушиться при його твердінні.
Це твердження часто називають принципом затвердіння.
З цього принципу випливає, що умови рівноваги для твердого тіла є необхідними (але не достатніми!) умовами рівноваги деформованого тіла.
5. Аксіома паралелограма.
Рівнодійна двох сил, прикладених в одній точці твердого тіла, зображується діагоналлю паралелограма, побудованого на даних силах (рис. 16).
Складання за правилом паралелограма в математиці називається векторною (геометричною) сумою і записується так:
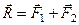 . (1.3)
. (1.3)
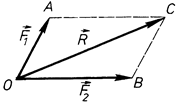 Рис. 16
Рис. 16
| 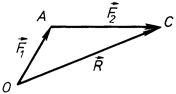 Рис. 17
Рис. 17
|
Рівність (1.3) виражає аксіому паралелограма сил, згідно з якою рівнодійна двох сил дорівнює векторній сумі заданих сил. Очевидно, додавання за правилом паралелограма можна замінити додаванням за правилом трикутника (рис. 17).
Величину рівнодійної можна визначити за теоремою косинусів. З 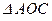 (рис. 16) маємо
(рис. 16) маємо
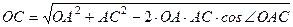 .
.
 Оскільки
Оскільки 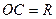 ,
, 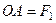 ,
, 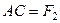 ,
, 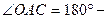
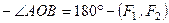 , отримаємо
, отримаємо
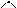
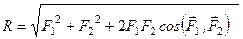 . (1.4)
. (1.4)
За формулою (1.4) обчислюють модуль рівнодійної двох сил, яка визначається за правилом паралелограма.
П’ята аксіома має широке практичне використання. По-перше, на основі даної аксіоми дію двох сил, прикладених в одній точці, можна замінити однією силою (рівнодійною). По-друге, на основі даної аксіоми вектор кожної сили можна розкласти по двох заданих напрямах, які проходять через точку прикладання сили.
Шостою аксіомою статики є аксіома про звільнення від в’язей, тобто принцип звільнення від в’язей, який був сформульований в § 5.
На основі аксіоми 5 доведемо теорему (лему) про рівно-вагу трьох сил:
три непаралельні сили, які діють на тверде тіло в одній площині, зрівноважуються тільки в тому випадку, коли лінії їх дії перетинаються в одній точці.
Доведення. Нехай на тверде тіло в точках  ,
,  ,
, 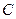 діють три непаралельні сили
діють три непаралельні сили 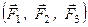 , які розміщені в площині рисунка (рис. 18, а, де вказані тільки сили
, які розміщені в площині рисунка (рис. 18, а, де вказані тільки сили 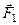 і
і 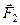 і точки їх прикладання).
і точки їх прикладання).
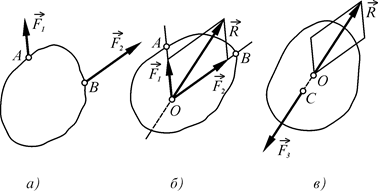
Рис. 18
Знаходимо точку перетину ліній дій сил 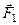 і
і 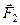 (точку
(точку  ) і перенесемо дані сили в точку
) і перенесемо дані сили в точку  (адже сила – це ковзний вектор). Згідно з аксіомою 5 знаходимо їх рівнодійну
(адже сила – це ковзний вектор). Згідно з аксіомою 5 знаходимо їх рівнодійну 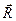 (рис. 18, б). Таким чином, на тверде тіло тепер діють тільки дві сили: знайдена рівнодійна
(рис. 18, б). Таким чином, на тверде тіло тепер діють тільки дві сили: знайдена рівнодійна 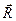 і сила
і сила 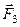 , яка ще не вказана на рисунку. Згідно з теоремою, яка доводиться, сили повинні бути зрівноважені, отже (аксіома 1) сили
, яка ще не вказана на рисунку. Згідно з теоремою, яка доводиться, сили повинні бути зрівноважені, отже (аксіома 1) сили 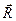 і
і 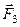 повинні мати спільну лінію дії, тоді точка прикладання
повинні мати спільну лінію дії, тоді точка прикладання 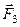 (точка
(точка 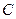 ) знаходиться на лінії дії сили
) знаходиться на лінії дії сили 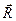 , а саме сила
, а саме сила 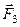 діє на тверде тіло, як вказано на рис. 18, в. Таким чином, лінії дії трьох сил перетинаються в одній точці.
діє на тверде тіло, як вказано на рис. 18, в. Таким чином, лінії дії трьох сил перетинаються в одній точці.
Однак треба відзначити, що теорема про три сили є тільки необхідною умовою зрівноваження трьох сил. Її часто використовують для визначення лінії дії реакції в’язі, напрям якої згідно з класифікацією в’язей невідомий.
Приклад. Визначити лінію дії реакції циліндричного шарніра  , навколо якого може обертатись однорідний стрижень
, навколо якого може обертатись однорідний стрижень 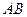 вагою
вагою 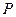 , що опирається на ребро
, що опирається на ребро 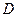 (рис. 19, а).
(рис. 19, а).
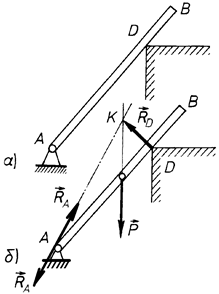
Рис. 19
Стрижень 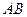 знаходиться в рівновазі. На нього діють тільки три сили: 1) сила ваги
знаходиться в рівновазі. На нього діють тільки три сили: 1) сила ваги 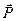 , яка прикладена в середині стрижня і напрямлена по вертикалі вниз; 2) реакція ребра
, яка прикладена в середині стрижня і напрямлена по вертикалі вниз; 2) реакція ребра 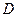 –
– 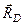 , яка перпендикулярна до поверхні стрижня; 3) реакція шарніра
, яка перпендикулярна до поверхні стрижня; 3) реакція шарніра  –
– 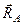 , яка невідома за напрямом. Напрям залежить від дії прикладених сил, тобто є невідомим. Але лінію дії
, яка невідома за напрямом. Напрям залежить від дії прикладених сил, тобто є невідомим. Але лінію дії 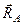 легко визначити за теоремою про три сили. Для цього знаходимо точку перетину ліній дій сил
легко визначити за теоремою про три сили. Для цього знаходимо точку перетину ліній дій сил 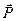 і
і 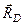 – точку
– точку  . У відповідності до доведеної теореми реакція
. У відповідності до доведеної теореми реакція 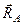 буде напрямлена по прямій
буде напрямлена по прямій 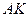 , бо для рівноваги трьох сил необхідно, щоб лінії їх дії перетинались в одній точці. В який бік? Це вже інше питання, на яке поки що відповісти не можемо. Для цього потрібно знати не тільки необхідну, а й достатню умову зрівноваження трьох сил.
, бо для рівноваги трьох сил необхідно, щоб лінії їх дії перетинались в одній точці. В який бік? Це вже інше питання, на яке поки що відповісти не можемо. Для цього потрібно знати не тільки необхідну, а й достатню умову зрівноваження трьох сил.
Розглянуті аксіоми, а також основні поняття статики дають змогу приступити до розв’язання основних задач статики для найпростішої системи сил – системи збіжних сил.
1.1 Система збіжних сил
Система збіжних сил – це система сил, лінії дії яких перетинаються в одній точці.
§ 7 Зведення системи збіжних сил
до канонічного вигляду
Нехай на тверде тіло діє система сил 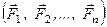 (рис. 20 а). Діюча система сил є збіжною, бо лінії дії всіх сил перетинаються в одній точці – точці
(рис. 20 а). Діюча система сил є збіжною, бо лінії дії всіх сил перетинаються в одній точці – точці  . Оскільки сила – це ковзний вектор, перенесемо всі сили до точки
. Оскільки сила – це ковзний вектор, перенесемо всі сили до точки  (рис. 20 б). Таким чином, ми отримали систему сил, прикладених до однієї точки. Вона еквівалентна заданій системі сил.
(рис. 20 б). Таким чином, ми отримали систему сил, прикладених до однієї точки. Вона еквівалентна заданій системі сил.
На основі аксіоми паралелограма сил проведемо послідовне додавання сил (див. рис. 20 в, де для наочності додавання проведено за правилом трикутника). Спочатку додаємо сили 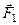 і
і 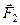 і знаходимо рівнодійну
і знаходимо рівнодійну 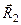
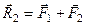 (а)
(а)
(індекс в позначенні рівнодійної відповідає кількості доданих сил).
Далі додаємо 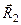 і
і 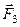 (будуючи знову трикутник цих сил) і знаходимо рівнодійну
(будуючи знову трикутник цих сил) і знаходимо рівнодійну 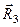
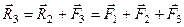 . (б)
. (б)
Продовжуючи додавання, дійдемо до останньої сили і отримаємо
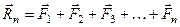 , (в)
, (в)
тобто замість системи 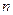 сил, що діяли на тверде тіло, ми отримали силу, дія якої еквівалентна вихідній системі сил.
сил, що діяли на тверде тіло, ми отримали силу, дія якої еквівалентна вихідній системі сил.
Таким чином, для системи збіжних сил розв’язана перша основна задача статики – систему збіжних сил зведено до канонічного вигляду.
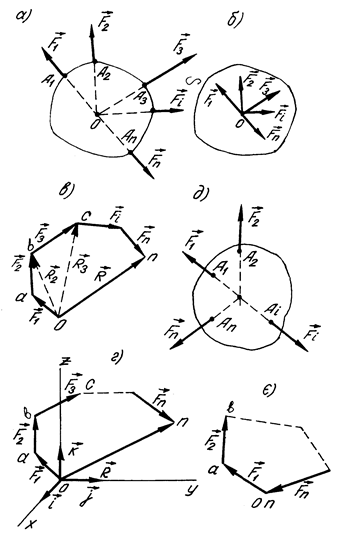
Рис. 20
Канонічним виглядом системи збіжних сил є одна сила (рівнодійна)
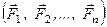
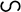
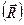 . (1.5)
. (1.5)
До того ж, як видно з векторної рівності (в), рівнодійна системи збіжних сил дорівнює геометричній сумі всіх сил системи
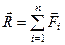 . (1.6)
. (1.6)
Векторний багатокутник 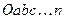 (рис. 20 в), отриманий при складанні сил, в теоретичній механіці називається силовим.
(рис. 20 в), отриманий при складанні сил, в теоретичній механіці називається силовим.
На основі векторної рівності (1.6) можна встановити два способи визначення рівнодійної.
1. Геометричний спосіб визначення рівнодійної.
Щоб геометрично (шляхом однієї побудови) визначити рівнодійну, необхідно скласти всі сили, тобто побудувати силовий багатокутник (рис. 20 г). Зауважимо, що додавання сил можна проводити в будь-якій послідовності. Замикаюча сторона силового багатокутника, яка напрямлена проти його обходу, визначає рівнодійну як за величиною, так і за напрямом (рис. 20 г).
2. Аналітичний спосіб визначення рівнодійної.
З математики відомо, що кожну векторну рівність можна спроектувати на вісь. При проектуванні векторної рівності на вісь знак рівності зберігається, а проекція геометричної суми на вісь дає алгебраїчну суму відповідних проекцій векторів на задану вісь.
Спроектувавши рівність (1.6) на координатні осі, які вказані на рис. 20 г, отримаємо
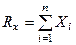 ;
; 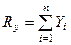 ;
; 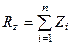 . (1.7)
. (1.7)
Формули (1.7) визначають проекції рівнодійної системи сил на декартові осі координат. В даних формулах 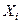 ,
, 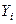 ,
, 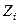 – проекції
– проекції 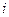 -ої сили (
-ої сили ( 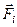 ) системи на декартові осі координат. Згідно з цими формулами маємо, що
) системи на декартові осі координат. Згідно з цими формулами маємо, що
проекція рівнодійної системи сил на вісь дорівнює алгебраїчній сумі проекцій всіх сил системи на дану вісь.
Оскільки формули (1.7) визначають проекції рівнодійної на три взаємно перпендикулярні осі, то модуль її обчислюється за формулою
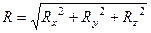 . (1.8)
. (1.8)
Напрям вектора рівнодійної визначається кутами, які утворює вектор з координатними осями. З визначення поняття “проекція на вісь” (див. додаток 2) маємо
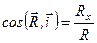 ;
; 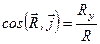 ;
; 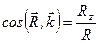 . (1.9)
. (1.9)
Формули (1.9) визначають напрямні косинуси вектора рівнодійної, а сукупність формул (1.7)–(1.9) аналітично визначає вектор рівнодійної.
§ 8 Умови і рівняння рівноваги
системи збіжних сил
За визначенням зрівноваженої системи сил маємо
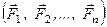
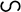
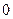 . (а)
. (а)
Для системи збіжних сил (див. 1.5) отримали
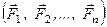
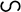
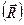 . (б)
. (б)
Порівнюючи еквівалентності (а) і (б), отримаємо:
для рівноваги системи збіжних сил необхідно і достатньо, щоб її рівнодійна дорівнювала нулеві
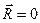 . (1.10)
. (1.10)
Векторна рівність (1.10) є необхідною і достатньою умовою рівноваги системи збіжних сил. З даної умови випливає:
1. Геометрична умова рівноваги.
Як відомо, рівнодійна – це замикаюча сторона силового багатокутника (рис. 20 г). Отже, умова (1.10) буде виконуватись тільки тоді, коли остання вершина силового багатокутника суміститься з першою вершиною, тобто силовий багатокутник буде замкнутим.
Таким чином,
необхідною і достатньою умовою рівноваги системи збіжних сил (рис. 20 в) є замкнутість її силового багатокутника (рис. 20 є).
2. Аналітичні умови рівноваги. Рівняння рівноваги.
Згідно з формулою (1.8), котра визначає модуль рівнодійної, умова (1.10) буде виконуватись тільки тоді, коли 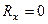 ,
, 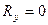 ,
, 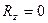 , а це означає (див. формулу 1.7), що
, а це означає (див. формулу 1.7), що
для рівноваги системи збіжних сил необхідно і достатньо, щоб суми проекцій цих сил на три взаємно перпендикулярні осі дорівнювали нулеві
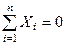 ;
; 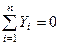 ;
; 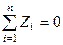 . (1.11)
. (1.11)
Очевидно, для плоскої системи збіжних сил матимемо
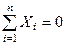 ;
; 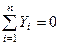 . (1.12)
. (1.12)
Таким чином, для системи збіжних сил умова рівноваги (1.10) має дві форми: геометричну – це замкнутий силовий багатокутник і аналітичну – це виконання рівності (1.11). Отже, задачі на рівновагу системи збіжних сил можна розв’язу-вати двома способами – геометрично і аналітично. Перший спосіб зручний для плоскої системи збіжних сил.
Аналітичні умови рівноваги (1.11) чи (1.12) розписані для конкретної задачі, в які входять невідомі параметри (реакції в’язей, активні сили, відстані, кути і т. ін.), називаються рівняннями рівноваги.
§ 9 Алгоритм розв’язання задач на рівновагу
Всі задачі на рівновагу матеріального об’єкта, незважаючи на те, яка система діє на нього, бажано розв’язувати за таким алгоритмом.
1. Виділити матеріальний об’єкт (точку, тверде тіло, систему твердих тіл), рівновага якого буде розглядатись.
2. До виділеного матеріального об’єкта прикласти всі активні сили.
3. Користуючись принципом звільнення від в’язей, відкинути в’язі, які накладені на виділений об’єкт, замінивши їх дію відповідними реакціями.
4. Залежно від отриманої системи сил вибрати відповідні умови рівноваги.
5. Скласти рівняння рівноваги.
6. З отриманих рівнянь знайти шукані величини.
(Див. додаток 3, в якому розглянуті відповідні приклади.)
Питання для самоконтролю
1. Яка система сил називається збіжною?
2. До якого канонічного вигляду зводиться збіжна система сил?
3. Сформулюйте необхідну і достатню умову рівноваги збіжної системи сил.
4. Запишіть аналітичні умови рівноваги просторової системи збіжних сил.
5. Сформулюйте геометричну умову рівноваги системи збіжних сил.
6. Запишіть аналітичні умови рівноваги плоскої системи збіжних сил.
7. Сформулюйте теорему про три сили.
8. За теоремою про три сили вкажіть лінію реакції циліндричного шарніра  (рис. А).
(рис. А).
9. Визначіть величину рівнодійної двох рівних за модулем сил 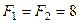 Н, які прикладені до однієї точки, утворюючи між собою кут 60°.
Н, які прикладені до однієї точки, утворюючи між собою кут 60°.
10. Визначіть величину і напрям рівнодійної системи сил (рис. Б), якщо 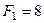 Н,
Н, 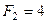 Н.
Н.
11. Для системи збіжних сил 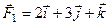 ,
, 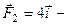
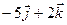 ,
, 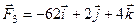 визначіть величину і напрям рівнодійної.
визначіть величину і напрям рівнодійної.
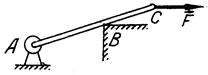 Рис. А
Рис. А
| 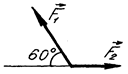 Рис. Б
Рис. Б
|
12. Кут між силами 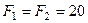 Н, які прикладені до однієї точки, дорівнює 120°. Визначіть модуль сили
Н, які прикладені до однієї точки, дорівнює 120°. Визначіть модуль сили 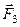 , яка зрівноважить задані сили.
, яка зрівноважить задані сили.
13. Вздовж діагоналі куба діє сил 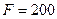 Н. Визначіть її проекції на координатні осі, початок яких знаходиться в точці прикладання сили і які напрямлені вздовж ребер куба.
Н. Визначіть її проекції на координатні осі, початок яких знаходиться в точці прикладання сили і які напрямлені вздовж ребер куба.
1.2 Теорія моменту сил
Практика підказує, що коли силу прикласти до твердого тіла, котре має закріплену точку або вісь обертання, то під дією даної сили тіло почне обертатись. Обертальна дія сили на тіло характеризується її моментом, а тому введемо нові поняття: момент сили відносно точки, момент сили відносно осі.
§ 10 Момент сили відносно точки
Нехай нам задано силу  , яка прикладена в точці
, яка прикладена в точці  , і якась інша точка
, і якась інша точка  , котра не знаходиться на лінії дії сили (рис. 21, а).
, котра не знаходиться на лінії дії сили (рис. 21, а).
Введемо поняття алгебраїчного і векторного моменту сили  відносно точки
відносно точки  .
.
Алгебраїчним моментом сили відносно точки назива-ється добуток, взятий з відповідним знаком, модуля сили на її плече.
Плече сили – це довжина перпендикуляра, опущеного з точки на лінію дії сили. Плечем заданої сили  відносно точки
відносно точки  буде відстань
буде відстань 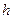 – довжина перпендикуляра
– довжина перпендикуляра 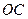 (рис. 21, б).
(рис. 21, б).
Якщо позначити момент сили  відносно точки
відносно точки 
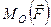 , то згідно з визначенням і рис. 21, б маємо
, то згідно з визначенням і рис. 21, б маємо
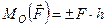 . (1.13)
. (1.13)
Формула (1.13) визначає момент сили відносно точки. Як в даній формулі вибираються знаки? Кожна наука цей знак вибирає по-своєму. В теоретичній механіці прийнято, що знак “+” береться в тому випадку, коли з боку спостерігача видно, що сила намагається повернути тіло проти руху годинникової стрілки. В протилежному випадку береться знак “–“. Так (див. рис. 21, в),
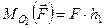 ,
, 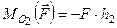 .
.
З формули (1.13) видно, що 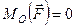 у випадку, коли
у випадку, коли 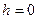 , а це можливо тільки тоді, коли точка
, а це можливо тільки тоді, коли точка  знаходиться на лінії дії сили. Отже, якщо лінія дії сили проходить через точку, то момент заданої сили відносно цієї точки дорівнює нулеві.
знаходиться на лінії дії сили. Отже, якщо лінія дії сили проходить через точку, то момент заданої сили відносно цієї точки дорівнює нулеві.
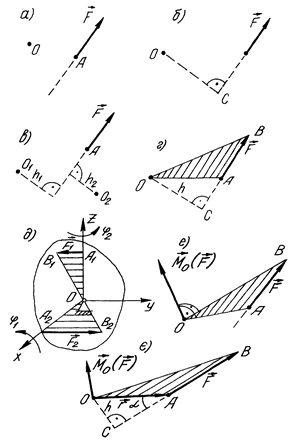
Рис. 21
З’єднаємо точку  з початком і кінцем вектора сили
з початком і кінцем вектора сили  . Отримаємо трикутник
. Отримаємо трикутник 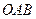 . Оскільки
. Оскільки 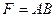 , а
, а 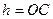 , то
, то 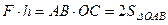 . Отже,
. Отже,
момент сили відносно точки чисельно дорівнює
подвійній площі трикутника, вершинами якого є точка і початок та кінець сили
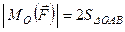 . (1.14)
. (1.14)
Формула (1.13), яка визначає момент сили відносно точки, має суттєвий недолік – вона не враховує положення площини трикутника 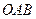 (рис. 21, г), від якого залежить обертальна дія сили. Адже, як показує детальний аналіз, під дією сили
(рис. 21, г), від якого залежить обертальна дія сили. Адже, як показує детальний аналіз, під дією сили  (рис. 21, д) тіло фактично намагається повернутись навколо осі, яка перпендикулярна до площини, що проходить через силу і точку. Отже, щоб повністю охарактеризувати дію сили на тверде тіло, яке має закріплену точку, бажано для визначення моменту сили відносно точки мати формулу, яка враховувала б величину сили, її плече (це враховує формула 1.13) і яка вказувала б вісь, навколо якої намагається повернутися тіло.
(рис. 21, д) тіло фактично намагається повернутись навколо осі, яка перпендикулярна до площини, що проходить через силу і точку. Отже, щоб повністю охарактеризувати дію сили на тверде тіло, яке має закріплену точку, бажано для визначення моменту сили відносно точки мати формулу, яка враховувала б величину сили, її плече (це враховує формула 1.13) і яка вказувала б вісь, навколо якої намагається повернутися тіло.
А тому введемо поняття векторного моменту (вектор-моменту) сили відносно точки.
Векторний момент сили відносно точки – це вектор, перпендикулярний до площини, котра проходить через силу і точку, і напрямлений в бік, звідки видно, що сила намагається повернути тіло проти руху годинникової стрілки (рис. 21, е).
Величина цього вектора дорівнює
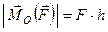 .
.
Легко отримати формулу, яка визначає вектор моменту сили 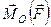 відносно точки. Для цього проведемо вектор
відносно точки. Для цього проведемо вектор 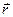 (див. рис. 21, є) з центра
(див. рис. 21, є) з центра  в точку
в точку  , в якій прикладено силу
, в якій прикладено силу  . Цей вектор, який визначає положення однієї точки відносно другої, надалі будемо називати радіус-вектором. З трикутника
. Цей вектор, який визначає положення однієї точки відносно другої, надалі будемо називати радіус-вектором. З трикутника 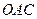 (рис. 21, є) видно, що
(рис. 21, є) видно, що
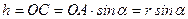 .
.
Тоді
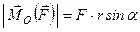 . (а)
. (а)
Враховуючи, що 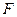 і
і 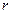 – модулі відповідних векторів, а
– модулі відповідних векторів, а 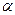 – кут між ними, формула (а) визначає модуль векторного добутку векторів
– кут між ними, формула (а) визначає модуль векторного добутку векторів  і
і 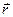 , тобто
, тобто
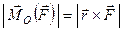 . (б)
. (б)
Порядок перемноження векторів у формулі (б) вибрано на основі властивостей векторного добутку. Відкинувши в формулі (б) модуль, отримаємо формулу, яка визначає вектор моменту сили відносно точки і враховує всі фактори, від яких залежить обертальна дія сили: величину сили, її точку прикладання, положення сили відносно точки
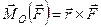 . (1.15)
. (1.15)
Отже,
вектор моменту сили відносно точки (центра) геометрично дорівнює векторному добутку радіуса-вектора точки прикладання сили відносно центра на вектор сили.
Алгебраїчним моментом сили відносно точки користуються при дії на механічну систему плоскої системи сил, векторним – у випадку дії просторової системи сил.
§ 11 Момент сили відносно осі
Момент сили відносно осі – це алгебраїчна величина, яка дорівнює алгебраїчному моменту проекції сили на площину, перпендикулярну до осі, відносно точки перетину осі з площиною: 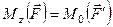 .
.
Отже, щоб визначити момент сили  відносно осі
відносно осі  (рис. 22, а), необхідно:
(рис. 22, а), необхідно:
1. Провести площину, перпендикулярну до осі (на рис. 22, б такою площиною є площина 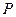 , а точка
, а точка  – це точка перетину осі з площиною).
– це точка перетину осі з площиною).
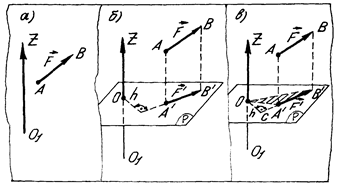
Рис. 22
2. Вектор сили  спроектувати на задану площину. Як відомо (див. додаток 1), проекція сили на площину – це вектор. В даному випадку (рис. 22, б) – це вектор
спроектувати на задану площину. Як відомо (див. додаток 1), проекція сили на площину – це вектор. В даному випадку (рис. 22, б) – це вектор 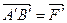 .
.
3. Отриману проекцію 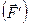 помножити на найкоротшу відстань від точки перетину осі з площиною до лінії дії цієї проекції і вибрати відповідний знак
помножити на найкоротшу відстань від точки перетину осі з площиною до лінії дії цієї проекції і вибрати відповідний знак
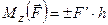 . (1.16)
. (1.16)
Знак вибирається згідно з означенням алгебраїчного моменту сили 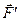 або з таких міркувань: якщо, дивлячись з кінця осі, спостерігач бачить намагання сили повернути площину проти руху годинникової стрілки, то береться знак “+”; в протилежному випадку – знак “–“. В нашому випадку (рис. 22) треба брати знак “+”.
або з таких міркувань: якщо, дивлячись з кінця осі, спостерігач бачить намагання сили повернути площину проти руху годинникової стрілки, то береться знак “+”; в протилежному випадку – знак “–“. В нашому випадку (рис. 22) треба брати знак “+”.
З формули (1.16) випливає, що момент сили відносно осі дорівнює нулеві в двох випадках:
1) 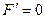 , а це буде тоді, коли сила паралельна до осі (рис. 23, а);
, а це буде тоді, коли сила паралельна до осі (рис. 23, а);
2) 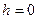 – лінія дії сили проходить через вісь (рис. 23, б).
– лінія дії сили проходить через вісь (рис. 23, б).
Треба також відзначити, що момент сили відносно осі – це скалярна величина, яка графічно зображується у вигляді відрізка, котрий відкладається вздовж осі. Якщо 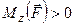 , то цей відрізок відкладається в додатному напрямі осі (рис. 23, в), при
, то цей відрізок відкладається в додатному напрямі осі (рис. 23, в), при 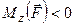 – у від’ємному її напрямі (рис. 23, г).
– у від’ємному її напрямі (рис. 23, г).
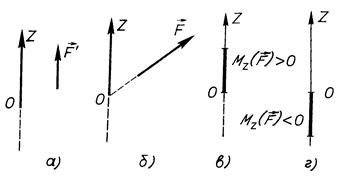
Рис. 23
Оскільки( див. рис. 22, в) 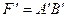 є основою трикутника
є основою трикутника 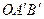 , а
, а 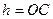 – його висота, то
– його висота, то 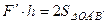 і отримуємо
і отримуємо
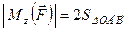 , (1.17)
, (1.17)
момент сили відносно осі чисельно дорівнює подвійній площі трикутника, вершинами якого є початок і кінець вектора проекції сили на площину, перпендикулярну до осі, і точка перетину осі з пло-щиною (рис. 22, в).
§ 12 Залежність між моментом сили відносно точки
і моментом сили відносно осі, яка проходить через
цю точку
Для встановлення залежності між моментом сили відносно точки й моментом сили відносно осі, котра проходить через задану точку, розглянемо довільну силу  , яка прикладена в точці
, яка прикладена в точці  . Візьмемо будь-яку точку
. Візьмемо будь-яку точку  , через яку проведемо вісь
, через яку проведемо вісь 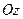 (рис. 24, а). Визначимо момент сили
(рис. 24, а). Визначимо момент сили  відносно точки
відносно точки  . Як було встановлено, моментом сили відносно точки є вектор
. Як було встановлено, моментом сили відносно точки є вектор 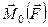 , перпендикулярний до площини
, перпендикулярний до площини 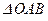 . Величина цього вектора за формулою (1.14) дорівнює
. Величина цього вектора за формулою (1.14) дорівнює
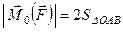 . (а)
. (а)
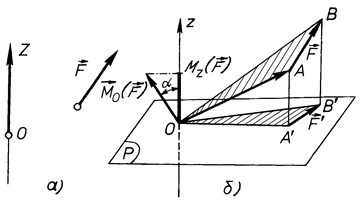
Рис. 24
Вказуємо цей вектор на рисунку (див. рис. 24, б). Тепер визначимо момент сили  відносно осі. Для цього силу
відносно осі. Для цього силу  спроектуємо на площину
спроектуємо на площину 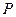 , яка проходить через точку
, яка проходить через точку  перпендикулярно до осі
перпендикулярно до осі 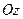 . Отримаємо вектор
. Отримаємо вектор 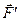 . Як було встановлено, момент сили відносно осі – це скалярна величина, яка чисельно визначається за формулою (див. 1.17)
. Як було встановлено, момент сили відносно осі – це скалярна величина, яка чисельно визначається за формулою (див. 1.17)
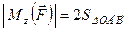 . (б)
. (б)
З рисунка 24, б видно, що трикутник 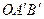 є проекцією трикутника
є проекцією трикутника 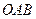 на площину
на площину 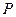 . З математики відомо, що площа проекції плоскої фігури на площину
. З математики відомо, що площа проекції плоскої фігури на площину 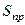 дорівнює площі фігури
дорівнює площі фігури 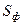 , помноженій на косинус кута між площинами фігури і проекції, тобто
, помноженій на косинус кута між площинами фігури і проекції, тобто
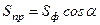 . (в)
. (в)
Застосувавши рівність (в) до трикутників 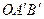 і
і 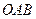 і помноживши обидві її частини на 2, дістанемо
і помноживши обидві її частини на 2, дістанемо
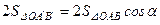 ,
,
або
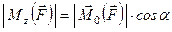 . (г)
. (г)
В отриманій залежності 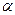 – це кут між площинами трикутників
– це кут між площинами трикутників 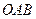 і
і 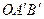 . Але кут між двома площинами дорівнює гострому куту між перпендикулярами до цих площин.
. Але кут між двома площинами дорівнює гострому куту між перпендикулярами до цих площин.
Якщо ввести кут між векторним моментом 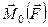 і додатним напрямом осі
і додатним напрямом осі 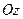 , то з врахуванням формули (г) можна записати
, то з врахуванням формули (г) можна записати
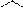
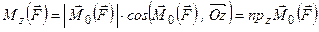 . (1.18)
. (1.18)
Рівність (1.18) дає залежність між моментом сили відносно точки і моментом сили відносно осі, котра проходить через задану точку, згідно з якою маємо:
момент сили відносно осі дорівнює проекції вектора моменту сили відносно точки, що знаходиться на осі, на задану вісь.
Отже, ми отримали ще один спосіб визначення моменту сили відносно осі. Згідно з цим способом, необхідно визначити вектор моменту сили відносно будь-якої точки даної осі і отриманий вектор спроектувати на цю вісь. Даний спосіб в практиці майже не використовується, бо момент сили відносно осі найлегше визначити за формулою (1.16). Зате в теоретичному курсі він часто використовується.
§ 13 Аналітичне визначення моменту сили
відносно довільної точки
На практиці часто зустрічаються задачі, в яких вимагається визначити момент сили, заданої своїми проекціями на координатні осі, відносно точки, положення якої задається координатами. Отримаємо відповідні формули. Для цього (див. рис. 25) розглянемо декартовий простір з координатними осями 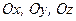 , яким відповідають орти
, яким відповідають орти 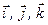 . Нехай в даному просторі в точці
. Нехай в даному просторі в точці  з координатами
з координатами 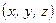 діє сила
діє сила  , проекції якої на координатні осі відповідно дорівнюють
, проекції якої на координатні осі відповідно дорівнюють 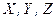 . Візьмемо довільну точку
. Візьмемо довільну точку 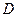 з координатами
з координатами 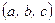 і визначимо момент сили
і визначимо момент сили  відносно цієї точки. За формулою (1.15) маємо
відносно цієї точки. За формулою (1.15) маємо
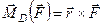 .
.
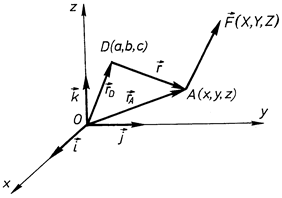
Рис. 25
З векторної алгебри відомо, що кожний векторний добуток можна представити у вигляді визначника. В нашому випадку
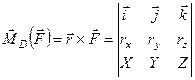 .
.
Розкривши визначник за елементами першого рядка, отримаємо
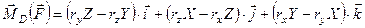 , (а)
, (а)
де 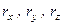 – проекції радіус-вектора
– проекції радіус-вектора 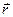 на координатні осі.
на координатні осі.
Згідно з рис. 25 маємо 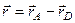 , отже
, отже
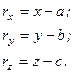 (б)
(б)
Сам вектор 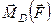 можна розкласти вздовж осей координат
можна розкласти вздовж осей координат
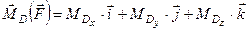 . (в)
. (в)
Співставляючи рівності (а) і (в) і враховуючи (б), отримаємо
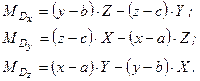 , (1.19)
, (1.19)
Формули (1.19) визначають проекції на декартові осі координат вектора моменту сили відносно точки 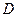 .
.
Знаючи проекції, за формулою
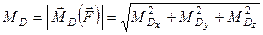 (1.20)
(1.20)
легко обчислюється модуль вектора моменту відносно точки 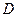 . Напрямні косинуси вектора
. Напрямні косинуси вектора 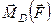 дорівнюють
дорівнюють
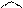
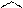
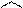
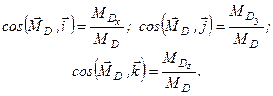 (1.21)
(1.21)
Отримані формули (1.19)–(1.21) аналітично визначають вектор моменту сили відносно довільної точки 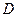 з координатами
з координатами 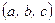 . Якщо точка
. Якщо точка 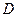 збігається з початком координат
збігається з початком координат 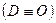 , тоді
, тоді 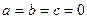 , і формули (1.19) набувають вигляду
, і формули (1.19) набувають вигляду
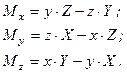 (1.22)
(1.22)
Формули (1.22) визначають проекції на координатні осі вектора моменту сили відносно початку координат. Дані формули мають і другий зміст – вони визначають момент сили відносно координатних осей, адже у відповідності з формулою (1.18) проекція вектора моменту сили відносно точки на вісь, яка проходить через дану точку, дорівнює моменту цієї сили відносно даної осі.
§ 14 Теорема Варіньйона
Теорема. Момент рівнодійної системи сил відносно довільної точки дорівнює геометричній сумі моментів всіх сил системи відносно даної точки, а момент рівнодійної системи сил відносно осі дорівнює алгебраїчній сумі момен-тів всіх сил системи відносно даної осі.
 Доведення.Сформульована теорема справедлива для будь-якої системи сил, яка має рівнодійну. Доведення теореми проведемо лише для збіжної системи сил, яка, як відомо, має рівнодійну. Доведення цієї теореми для загального випадку приведене в § 22.
Доведення.Сформульована теорема справедлива для будь-якої системи сил, яка має рівнодійну. Доведення теореми проведемо лише для збіжної системи сил, яка, як відомо, має рівнодійну. Доведення цієї теореми для загального випадку приведене в § 22.
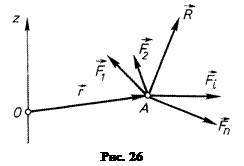
Нехай сили 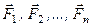 даної системи прикладені до точки
даної системи прикладені до точки  (рис. 26).
(рис. 26).
До цієї ж точки буде прикладена і рівнодійна 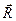 заданої системи сил. Визначимо її момент відносно довільної точки
заданої системи сил. Визначимо її момент відносно довільної точки 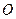 . З визначення моменту сили відносно точки (формула 1.15) маємо
. З визначення моменту сили відносно точки (формула 1.15) маємо
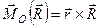 .
.
Оскільки 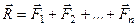 , то отримаємо
, то отримаємо
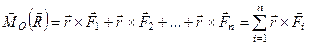 .
.
Але
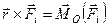 ,
,
тоді
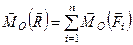 , (1.23)
, (1.23)
що і вимагалось довести в першій частині теореми Варіньйона.
Спроектувавши векторну рівність (1.23) на вісь 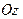
(рис. 26) і знаючи, що:
1) проекція вектора моменту сили відносно точки на вісь, що проходить через дану точку, дорівнює моменту заданої сили відносно цієї осі;
2) проекція векторної суми на вісь дорівнює алгебраїчній сумі відповідних проекцій,
отримаємо рівність, яку необхідно було довести в другій частині теореми Варіньйона
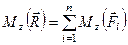 . (1.24)
. (1.24)
Примітки.
1. Теорема Варіньйона доведена для найпростішої системи сил – збіжної, бо нам поки що відомо єдину систему сил, яка зводиться до рівнодійної. Такою системою є система збіжних сил. Проте вона має місце для будь-якої системи сил, яка зводиться до рівнодійної.
2. Якщо сили і точка 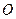 розміщені в одній площині, то їх вектори моментів сил перпендикулярні до цієї площини, тобто вони лежать на одній прямій і рівність (1.23) можна записати у вигляді
розміщені в одній площині, то їх вектори моментів сил перпендикулярні до цієї площини, тобто вони лежать на одній прямій і рівність (1.23) можна записати у вигляді
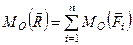 . (1.25)
. (1.25)
Отже,
алгебраїчний момент рівнодійної плоскої системи сил відносно довільної точки, яка знаходиться в площині дії сил, дорівнює алгебраїчній сумі моментів складових сил відносно даної точки.
3. Теорема Варіньйона має широке практичне використання. На практиці її використовують там, де визначення моменту сили ускладнене через трудність визначення її плеча. У цих випадках діють так: силу розкладають на складові, для яких легко визначаються плечі, і момент даної сили визначають як суму моментів її складових.
Приклад. Визначити момент сили  Н (див.
Н (див.
рис. 27) відносно точки 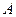 , якщо
, якщо 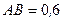 м,
м, 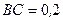 м.
м.
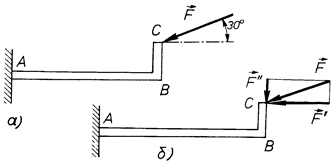
Рис. 27
Розв’язання. Для визначення моменту сили 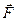 відносно точки
відносно точки 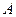 розкладемо її на складові
розкладемо її на складові 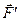 і
і 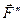 (див. рис. 27, б), причому
(див. рис. 27, б), причому
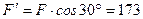 Н;
Н;
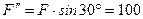 Н.
Н.
Момент сили 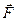 відносно точки
відносно точки 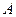 визначимо як суму моментів її складових
визначимо як суму моментів її складових
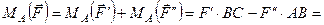
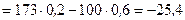 Н×м.
Н×м.
Питання для самоконтролю
1. Що називається моментом сили відносно точки?
2. Запишіть формулу, за допомогою якої визначається алгебраїчний момент сили відносно точки.
3. Чому прийнято момент сили відносно точки вважати вектором?
4. Який напрям має вектор моменту сили відносно точки?
5. Запишіть формулу, яка визначає вектор моменту сили відносно точки.
6. Визначіть момент сили 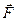 відносно точки
відносно точки 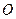 , якщо
, якщо  Н,
Н, 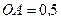 м. (рис. А).
м. (рис. А).
7. Що називається моментом сили відносно осі?
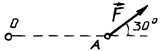 Рис. А
Рис. А
| 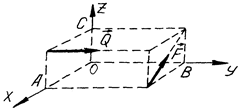 Рис. Б
Рис. Б
|
8. Запишіть формулу, за допомогою якої визначається момент сили відносно осі.
9. В яких випадках момент сили відносно осі дорівнює нулеві?
10. Як графічно зобразити момент сили відносно осі?
11. Визначіть моменти сил 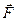 і
і  відносно координатних осей, якщо
відносно координатних осей, якщо 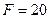 кН,
кН, 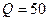 кН,
кН, 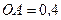 м,
м, 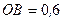 м,
м, 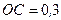 м. (рис. Б).
м. (рис. Б).
12. Запишіть формулу, яка відображає залежність між моментом сили відносно точки і моментом сили відносно осі, що проходить через задану точку.
13. Визначіть величину моменту сили 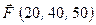 відносно початку осей координат, якщо задана сила прикладена в точці
відносно початку осей координат, якщо задана сила прикладена в точці 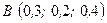 . Проекції сили на координатні осі задані в Ньютонах, а координати точки В – в метрах.
. Проекції сили на координатні осі задані в Ньютонах, а координати точки В – в метрах.
1.3 Довільна система сил
Перш ніж приступити до розв’язання основних задач теоретичного курсу статики для довільної системи сил введемо додаткові поняття.
§ 15 Головний вектор і головний момент системи сил
Поняття головного вектора і головного моменту системи сил є одним з основних понять теоретичної механіки. Це пояснюється, як Ви переконаєтесь в процесі вивчання теоретичного курсу, тим, що дія системи сил на тверде тіло визначається значенням її головного вектора і головного моменту.
Нехай задано довільну систему сил 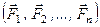 , які прикладені відповідно в точках
, які прикладені відповідно в точках 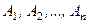 (рис. 28, а).
(рис. 28, а).
Головним вектором 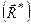 системи сил називається геометрична сума всіх сил системи
системи сил називається геометрична сума всіх сил системи
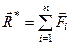 . (1.26)
. (1.26)
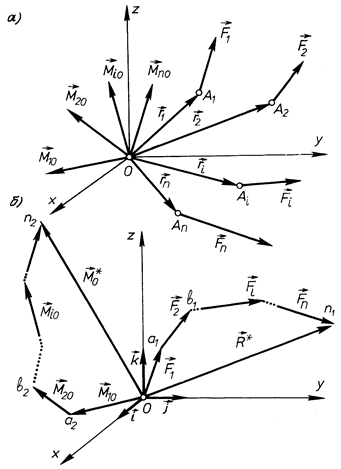
Рис. 28
До точок прикладання сил з центра 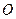 проведемо радіус-вектори
проведемо радіус-вектори 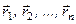 (рис. 28, а) і за формулою (1.13) визначимо момент кожної сили відносно центра
(рис. 28, а) і за формулою (1.13) визначимо момент кожної сили відносно центра 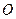 .
.
Головним моментом 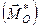 системи сил відносно довільної точки називається геометрична сума векторних моментів всіх сил системи відносно даної точки
системи сил відносно довільної точки називається геометрична сума векторних моментів всіх сил системи відносно даної точки
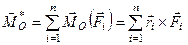 . (1.27)
. (1.27)
На основі формул (1.26–1.27) можна вказати два способи визначення головного вектора і головного моменту системи сил.
1. Геометричний спосіб
Щоб геометрично визначити головний вектор, необхідно векторно скласти всі сили системи, тобто побудувати силовий багатокутник 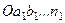 (рис. 28, б). Замикаюча сторона силово-го багатокутника, напрямлена проти його обходу, визначає як величину, так і напрям головного вектора заданої системи сил.
(рис. 28, б). Замикаюча сторона силово-го багатокутника, напрямлена проти його обходу, визначає як величину, так і напрям головного вектора заданої системи сил.
Аналогічно визначається і головний момент системи сил. Тільки тут будується багатокутник моментів 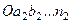 (рис. 28, в).
(рис. 28, в).
2. Аналітичний спосіб
Спроектувавши векторні рівності (1.26, 1.27) на декартові осі координат, отримаємо
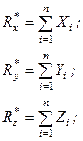 (1.28)
(1.28) 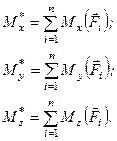 (1.29)
(1.29)
Формули (1.28) визначають проекції головного вектора на декартові осі координат. В цих формулах 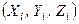 – проекції вектора
– проекції вектора 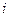 -ої сили системи на дані осі координат.
-ої сили системи на дані осі координат.
Формули (1.29) визначають проекції головного моменту системи сил на декартові осі координат. В даних формулах 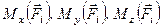 – проекції вектора моменту
– проекції вектора моменту 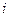 -ої сили системи на дані осі. Якщо головний момент системи визначено відносно початку координат, як це було зроблено за формулою (1.29), то відповідно до формули (1.18) можна сказати, що
-ої сили системи на дані осі. Якщо головний момент системи визначено відносно початку координат, як це було зроблено за формулою (1.29), то відповідно до формули (1.18) можна сказати, що 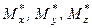 – це головні моменти відносно координатних осей, а
– це головні моменти відносно координатних осей, а 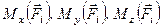 – це моменти сили
– це моменти сили 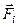 відносно координатних осей.
відносно координатних осей.
Знаючи проекції, знаходимо модуль головного вектора
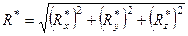 (1.30)
(1.30)
і головного моменту
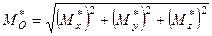 , (1.31)
, (1.31)
а також напрямні косинуси
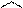
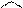
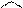
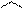
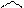
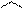
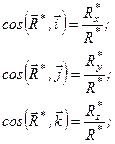 (1.32)
(1.32) 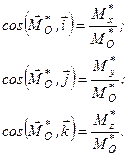 (1.33)
(1.33)
Формули (1.28), (1.30), (1.32) аналітично визначають головний вектор системи сил, а формули (1.29), (1.31), (1.33) – головний момент системи сил відносно точки 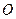 .
.
§ 16 Пара сил і її момент
Система двох рівних за величиною протилежно напря-млених сил ( 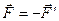 ), лінії дії яких не співпадають, називається парою сил (рис. 29).
), лінії дії яких не співпадають, називається парою сил (рис. 29).
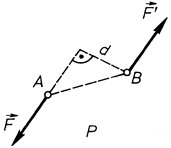 Рис. 29
Рис. 29
| 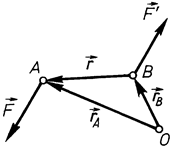 Рис. 30
Рис. 30
|
Основними характеристиками пари сил є:
1. Площина дії пари сил – це площина, в якій знаходиться пара сил. На рис. 29, на якому зображено пару сил 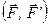 ,
, 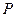 – це площина дії заданої пари сил. Вона єдина, оскільки через дві паралельні лінії можна провести тільки одну площину.
– це площина дії заданої пари сил. Вона єдина, оскільки через дві паралельні лінії можна провести тільки одну площину.
2. Плече пари сил – це найкоротша відстань між лініями дії сил пари. На рис. 29 воно позначено літерою 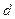 .
.
3. Момент пари сил.
Для введення поняття моменту пари сил розглянемо пару сил 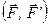 , сили якої прикладені в точках
, сили якої прикладені в точках 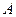 і
і 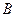 (рис. 30). Виберемо довільну точку
(рис. 30). Виберемо довільну точку 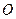 і проведемо відповідні радіуси-вектори
і проведемо відповідні радіуси-вектори 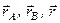 . За формулою (1.26) визначимо головний вектор пари сил
. За формулою (1.26) визначимо головний вектор пари сил
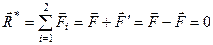 .
.
Отже, головний вектор пари сил дорівнює нулеві.
За формулою (1.27) визначимо головний момент пари сил відносно довільної точки 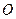
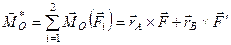 .
.
Оскільки 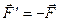 , отримаємо
, отримаємо
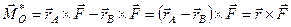 ,
,
тобто:
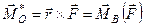 .
.
Головний момент пари сил не залежить від положення точки, відносно якої він визначається, а залежить тільки від параметрів самої пари сил і називається моментом пари сил.
Отже,
момент пари сил Дата добавления: 2015-06-10; просмотров: 2554;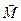 дорівнює векторному моменту однієї сили па
дорівнює векторному моменту однієї сили па
