Метод вероятностных графов

Согласно этому методу исследуемая звеньевая схема представляется в виде графа, конфигурация которого зависит от структуры схемы и режима искания, в котором используется схема.

Граф представляет собой картину всевозможных путей между заданным входом схемы и заданным выходом. Дуги графа соответствуют промежуточным линиям или маршрутам и выходам коммутационной системы. Вершины соответствуют точкам коммутации. Таким образом, процедура метода вероятностных графов заключается в том, чтобы записать функцию для вероятности потерь при установлении соединения. Обычно при составлении графа исследуемой системы используются простейшие типовые схемы:

W_i - вероятность занятости дуги, равная интенсивности нагрузки пропущенная линией или маршрутом, который характеризуется этой дугой.

Вероятность потерь в графе, состоящем из α-паралельно

параллельно включенных дуг: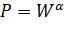

Вероятность потерь в графе, состоящем из -последовательно включенных дуг и вероятностями занятия этих

дуг: 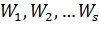соответственно, определяется выражением:

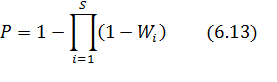
Граф типа П:

Рассмотрим пример построения вероятностного графа для различных трехзвенных схем (рис.6.1).

Рисунок 6.1 – Вероятностные графы для различных трехзвенных схем

Структура каждого графа отображает возможность пути установления соединений. Если для каждой дуги графа определить вероятность успешного установления пути, то между точками А и В можно определить возможность потери.

Например, для графа (а) на рисунке 6.1 используются обозначения:

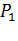- вероятность успешного создания пути между точками «А» и «2-1»;

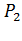- вероятность успешного создания пути между точками «А» и «2-2»;

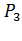- вероятность успешного создания пути между точками «2-1» и «3»;

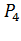- вероятность успешного создания пути между точками «2-2» и «3»;

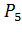- вероятность успешного создания пути между точками «3» и «В».

Тогда вероятность успешного установления пути между точками «А» и «3» будет определяться выражением:

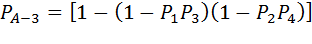(6.14)

Соответственно, занятость этого пути:

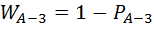(6.15)

Тогда искомая вероятность потери вызова между точками А и В будет определятся выражением:

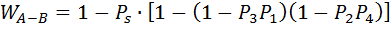(6.16)

Вероятность, определяемая по формуле (6.16) равна единице при следующих условиях:

1) нет свободных путей между вершинами «3» и «В» (или );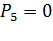

2) нет свободных путей между вершинами «2-1» и «А», а также между вершинами «2-2» и «3» ( .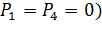

Анализируя представленный граф, можно сделать вывод, что для рассматриваемой модели наиболее важной является доступность пути между вершинами «3» и «В».

КОНТРОЛЬНЫЕ ВОПРОСЫ:

6.1.Перечислите аналитические методы расчета неполнодоступных включений.

6.2.В чем суть метода вероятностных графов?

6.3.Что представляет собой вероятностный граф?

6.4.Что представляет собой граф типа П?

6.5.Что представляет собой граф типа S?