Методы расчета однозвенных схем в системе с ожиданием

Рассматриваемая модель во многом аналогична первой задаче Эрланга, т.е. рассматривается коммутационная система, имеющая V - выходов, на которую поступает простейший поток вызовов с параметром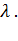

Время обслуживания одного вызова – случайная величина, распределенная по показательному закону со средним значением, принятым за единицу времени 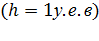,т.е.: .

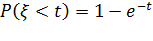Дисциплина обслуживания вызовов - с ожиданием, т.е. при занятости всех 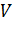- выходов, поступающий вызов становится в очередь и обслуживается по мере освобождения выходов.

Общее число вызовов, находящихся в системе на обслуживании и ожидающих: 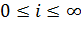- состояние коммутационной системы.

При 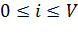величина характеризует число занятых линий в системе.

При число занятых линий равно 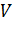, а разность между и 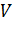- длина очереди: .

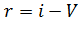Если 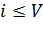( -состояние коммутационной системы) вероятность занятия равно -линий описывается формулой первого распределения Эрланга и складывается из вероятностей .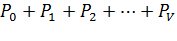

Если 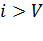вероятность того, что ожидаются 1,2,3,…, 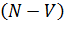вызовов, ,

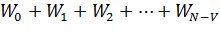где -вероятность состояния очереди (очереди нет):

(7.1)

Учитывая условие нормирования,

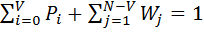, (7.2)

где 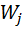- вероятность ожидания -го вызова.

При 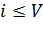уравнение статистического равновесия имеет вид:

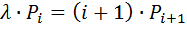(7.3)

При 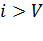уравнение статистического равновесия имеет вид:

(7.4)

Определим из (7.4) значение вероятности :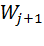

(7.5).

Будем подставлять в выражение (7.5) значения :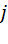

1) при - ;

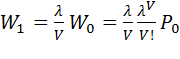2) при 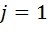- 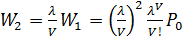; и т.д. ……… ;……

.

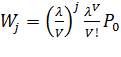В формуле (7.2) при 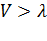и :

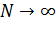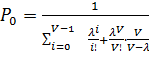(7.6)

Тогда вероятность наличия 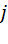ожидающих вызовов определяется по формуле:

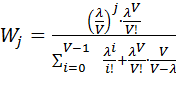(7.7)

Формула (7.7) носит название –второе распределение Эрланга.