ОБСЛУЖИВАНИЯ ВЫЗОВОВ

Имитационное или статистическое моделирование процессов обслуживания вызовов на ПЭВМ – это способ математического исследования систем коммутации. Он используется, когда не удается определить характеристики качества обслуживания аналитическими методами или когда требуется сравнить качество обслуживания конкретной коммутационной системой потока вызовов с теоретическими моделями.

При моделировании на ПЭВМ имитируется работа исследуемой коммутационной системы, т.е собирается , обрабатывается и выдается необходимая статистика об имитируемом процессе обслуживания вызовов.

В пределах изучаемой математической модели можно с любой заданной точностью воспроизвести исследуемый процесс и получить интересующие статистические характеристики.

Моделирование начинается с разработки задания на его проведение, где формируется цель и задача предстоящего исследования, определяются требования к точности и объему получаемых результатов.

Особое внимание должно уделяться оптимальному заданию исходных данных, по материалу задания разрабатывается алгоритм и пишется программа моделирования. Так как алгоритм моделирования должен отражать случайную природу имитируемого процесса обслуживания, то в его реализации используются случайные числа и события.

В структуре программы моделирования можно выделить:

a) информационную часть;

б) алгоритмическую часть.

Информационная часть отражает структуру и текущее состояние системы обслуживающей вызовы, содержит сведения о находящихся в системе вызовов и накапливаемых статистических характеристиках.

Алгоритмическая часть – это комплекс алгоритмов в процессе функционирования, которого меняются значения переменных информационной части.

Для имитации случайных величин используют стандартные подпрограммы (датчики) генерирующие псевдослучайные числа, т.е. такие числа, когда каждое число получается из предыдущего в результате применения арифметических или логических операций.

Эти числа называются псевдослучайными а не случайными, т.к. получаемые последовательности чисел являются периодическими. Период последовательности должен быть достаточным для требуемого объема статистических испытаний.

Обычно используют алгоритм для получения равномерно распределенных псевдослучайных величин, а затем, с помощью соответствующих преобразований, получают последовательности чисел с другими функциями распределения.

Для случая равномерного распределения в интервале 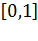псевдослучайное число 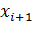может быть получено из предыдущего числа 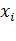с помощью соотношения:

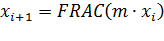,(9.1)

где 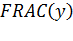- оператор дробной части от выражения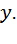

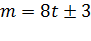,(9.2)

где - нечетное целое число.

Обычно перед использованием датчика псевдослучайных чисел задается начальное значение 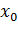на отрезке 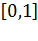. Задание разных значений 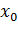позволяет формировать различные последовательности случайных величин.

Рассмотрим пример моделирования процесса обслуживания вызовов коммутационной системой математическая модель, которой ,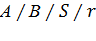

где А – тип распределения промежутков между вызовами;

В – тип распределения длительности обслуживания вызово;

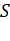– схема обслуживания;.

–число мест ожиданий. Для систем с явными потерями .

Обозначим:

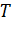- среднее время обслуживания вызова;

-время поступления очередного вызова;

-время окончания обслуживания очередного вызова.

Если 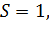т.е (однолинейная система), то этапы моделирования состоят в следующем:

1)

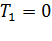
2) Моделируется время окончания обслуживания очередного состояния, учитывая тип распределения длительности обслуживания: ;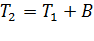

3) Моделируется момент поступления очередного вызова, учитывая тип распределения промежутков между вызовами.

4) Выполняется проверка: закончено ли моделирование, что реализуется сравнением 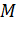(число поступивших вызовов) и 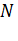(число вызовов, необходимых для моделирования). Сравнивая, и определяют, потерян вызов или обслужен.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

9.1.В чем состоит процесс моделирование случайных величин и событий ?

9.2.Из каких частей состоит программа моделирования ?

9.3.Из каких процедур состоит разработка алгоритмов моделирования

процессов обслуживания вызовов в телефонных сетях?

9.4.Составьте алгоритм моделирования процессов обслуживания вызовов в

системах с явными потерями.

9.5.Составьте алгоритм моделирования процессов обслуживания вызовов

в системах с ожиданием.

9.6.Составьте алгоритм моделирования процессов обслуживания вызовов в

системах с повторными вызовами.