РАЗДЕЛ 8 МЕТОДЫ РАСЧЕТА СИСТЕМ С ПОВТОРНЫМИ ВЫЗОВАМИ
Источники повторных вызовов могут быть проиллюстрированы с помощью модели, приведенной на рисунке 8.1.
Рисунок 8.1 – Распределение потерь по участкам телефонного тракта
Если обозначить через 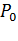 вероятность удачного соединения для абонента А, то соответствующая вероятность для неудачных попыток:
вероятность удачного соединения для абонента А, то соответствующая вероятность для неудачных попыток:
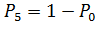 (8.1).
(8.1).
Причины повторных попыток вызовов объясняется потерями в процессе установления соединения. Характеристики повторения вызовов во многом определяются психологическими факторами.
Наличие повторных попыток искажает ряд классических представлений о функционирование сети телефонной связи. Статические наблюдения показали, что величина потерь вызовов в несколько раз может превосходить уровень, определяемый первой формулой Эрланга.
Одна из проблем анализа повторных попыток – сложность разделения потоков
первичных и повторных вызовов. На рисунке 8.2 показана соответствующая модель с указанием точек, в которых целесообразно производить измерения  . На самом деле обычно для измерения доступна только точка
. На самом деле обычно для измерения доступна только точка  .
.
Рисунок 8.2 – Модель системы с повторными вызовами
В таблице 8.1 представлены данные измерений успешных попыток по отношению к безуспешным соответственно для УАТС, ОПС(ГТС) и ЗТУ (рисунок 8.3.)
Рисунок 8.3- Фрагмент соединительного тракта на ГТС
Таблица 8.1Соотношение успешных и неуспешных попыток
| Тип исходящей попытки | Отношение успешных попыток к безуспешным | ||
| УАТС | ГТС | ЗТУ | |
| Успешная | 0,57 | 0,44 | 0,25 |
| Безуспешная | 0,43 | 0,56 | 0,75 |
| Блокировка | 0,04 | 0,29 | 0,56 |
| Ошибка набора | 0,02 | 0,06 | 0,06 |
| Абонент занят | 0,26 | 0,14 | 0,10 |
| Нет ответа | 0,11 | 0,07 | 0,03 |
Для расчета СМО с повторными вызовами разработано множество моделей и методов, ориентированных на использование таблиц и/или программных продуктов. Для простых моделей получены аналитические выражения.
Рассмотрим пример такой модели. Полнодоступная коммутационная система имеет 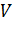 выходов, поступающий первичный поток вызовов - простейший с параметром
выходов, поступающий первичный поток вызовов - простейший с параметром 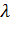 . Время обслуживания любого вызова – случайная величина, распределённая по показательному закону со средним значением единица.
. Время обслуживания любого вызова – случайная величина, распределённая по показательному закону со средним значением единица.
Поток повторных вызовов с параметром  :
:
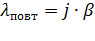 (8.2)
(8.2)
где j-число источников повторных вызовов;
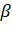 -интенсивность повторения вызова одним источником.
-интенсивность повторения вызова одним источником.
Предположим, что источник, послав первый вызов и получив отказ в соединение, с вероятностью  – повторяет его, а с вероятностью
– повторяет его, а с вероятностью  отказывается от дальнейших попыток установления соединения.
отказывается от дальнейших попыток установления соединения.
Аналогично для повторных вызовов обозначим 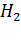 - вероятность повторения повторного вызова,
- вероятность повторения повторного вызова, 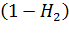 - отказ от повторения повторного вызова.
- отказ от повторения повторного вызова.
Величины  и
и 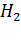 характеризуют меру настойчивости источника вызовов.
характеризуют меру настойчивости источника вызовов.
Состояние коммутационной системы будет определяться двумя параметрами:
 - число занятых выходов коммутационной системы(
- число занятых выходов коммутационной системы( 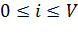 ) ;
) ;
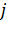 - число источников повторяющихся вызовов(
- число источников повторяющихся вызовов( 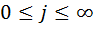 ).
).
Соответственно 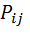 определяет вероятность состояния коммутационной системы в установившемся режиме.
определяет вероятность состояния коммутационной системы в установившемся режиме.
Изменение состояния системы за промежуток времени  возможно при осуществлении одного из следующих событий:
возможно при осуществлении одного из следующих событий:
1) поступление первичного вызова (вероятность поступления 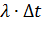 );
);
2) поступление повторного вызова (вероятность поступления  );
);
3) освобождение одного из занятых выходов 
В первом случае число занятых выходов ( 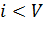 ) увеличивается на единицу. Во втором случае, одновременно с увеличением числа занятых выходов, уменьшается на единицу число источников повторных вызовов. В третьем случае уменьшается на единицу число занятых выходов.
) увеличивается на единицу. Во втором случае, одновременно с увеличением числа занятых выходов, уменьшается на единицу число источников повторных вызовов. В третьем случае уменьшается на единицу число занятых выходов.
Если первичный вызов поступит в состоянии 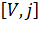 , то источник, получив отказ в соединении, перейдет в число повторяющего вызова с вероятностью
, то источник, получив отказ в соединении, перейдет в число повторяющего вызова с вероятностью  , величина
, величина 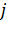 при этом, увеличивается на 1.
при этом, увеличивается на 1.
При поступлении в состоянии 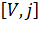 повторяющего вызова с вероятностью
повторяющего вызова с вероятностью 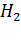 состояние коммутационной системы не изменяется (источник будет продолжать повторение вызовов). Соответственно с вероятностью
состояние коммутационной системы не изменяется (источник будет продолжать повторение вызовов). Соответственно с вероятностью 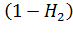 -величина
-величина 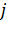 уменьшится на 1, а источник повторяющихся вызовов станет свободным.
уменьшится на 1, а источник повторяющихся вызовов станет свободным.
Для установившегося режима система уравнений вероятностей состояний исследуемой коммутационной системы будет иметь вид:
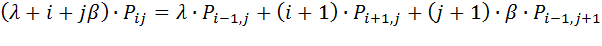 ,(8.3)
,(8.3)
где 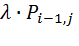 - вероятность поступления нового вызова от источника первичных
- вероятность поступления нового вызова от источника первичных
вызовов;
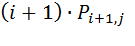 - вероятность освобождения одного выхода;
- вероятность освобождения одного выхода;
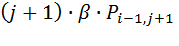 - вероятность поступления нового вызова от источника первичных вызовов и переход его в источник повторных вызовов.
- вероятность поступления нового вызова от источника первичных вызовов и переход его в источник повторных вызовов.
С учетом соответствующих вероятностей 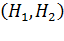 , уравнение (8.3) можно записать в следующем виде:
, уравнение (8.3) можно записать в следующем виде:
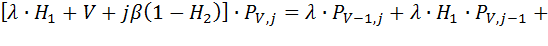
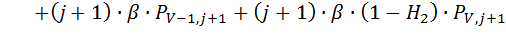 (8.4)
(8.4)
При условиях: 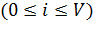 ; (
; ( 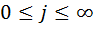 );
); 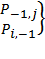 .- не существуют
.- не существуют
По условию нормирования ( 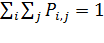 ) выражение (8.4) имеет вид:
) выражение (8.4) имеет вид:
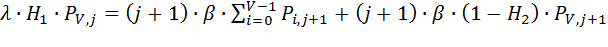 (8.5)
(8.5)
Полученное выражение позволяет определить основные характеристики качества обслуживания.
Дата добавления: 2017-02-20; просмотров: 660;
