Анализ межконцевых задержек

Для построения модели СМО, описывающей функционирование базовой сети с коммутацией пакетов, которая включает:

- М-каналов передачи данных и - W-узлов коммутации.

Введем ряд упрощающих предположений:

1) предположение о независимости, состоящее в том, что длина пакета, поступающего в канал, выбирается независимо в соответствии с плотностью распределения:

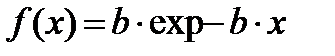, (10.1)

где 1/b- средняя длина пакета, измеряемая в битах (или байтах).

Данное предположение позволяет устранить зависимость между временами обслуживания в каналах.

Процесс поступления пакета в сеть является Пуассоновским с параметром

Λr[пак/час]. Здесь r- номер пары «узел источник» - «узел адресат».

Все пары упорядочены в соответствии с номерами 1,2,3,…R. Маршрут пакетов r-ого класса, т.е передаваемых в r-ой паре «источник – адресат», определяется матрицей:

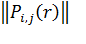(10.2),

где 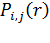- вероятность того, что пакет r-ого класса, закончивший обслуживание в

- ом канале, поступит потом в ый канал, причем 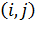будут принимать значение .

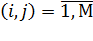Различные способы задания матрицы (10.2) определяют тип маршрутизации пакета в базовой сети. Например, при использовании постоянных виртуальных соединений и фиксированной маршрутизации, соответствущие значения для элементов 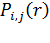могут принимать лишь два значения – «0» и «1»

2) объемы буферных накопителей не ограничены и подтверждение об успешной доставке пакета передается мгновенно.

Сделанные предположения позволяют полностью определить разомкнутую неоднородную СМО, моделирующую функционирование базовой сети передачи данных.

Сеть без источников и стоков (адресатов) называется замкнутой, в противном случае разомкнутой. Если заявки, циркулирующие в сети одного типа, то сеть называется однородной и наоборот.

Более общий случай неоднородной сети: каждый тип сообщения имеет свою функцию распределения длительности обслуживания в каждом УК, а так же свой закон перехода между узлами сети.

В рассматриваемую СМО поступает r- классов пуассоновских потоков пакетов с интенсивностью, 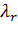, (причем 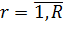) маршрут каждого из которых характеризуется матрицей (10.2).

Функция распределения длительности обслуживания пакетов r -го класса в

-ом УК СМО, которая моделирует канал передачи данных, являться экспоненциальной с параметром:

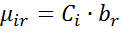, (10.3)

где 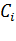- пропускная способность i-го канала, измеряемая в битах/секунду; 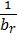- средняя длина пакета r -го класса.

Интенсивность потока пакетов r-го класса, поступающих в -ый канал, - ( 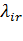) удовлетворяет уравнению баланса потоков:

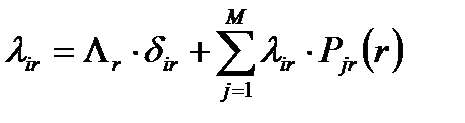, (10.4)

где 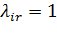, если входящий поток Λ_r поступит в i-ый канал;

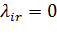, если входящий поток Λ_r не поступит в i-ый канал.

Общий поток пакетов, поступающих в i-ый канал:

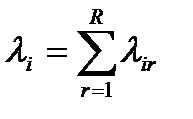(10.5)

Соответственно, общий поток пакетов,поступающих в сеть:

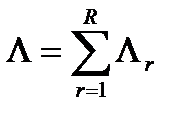(10.6)

Обозначим загрузку i-го канала пакетами -го класса через 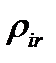, а общую загрузку i-го канала через 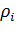,тогда

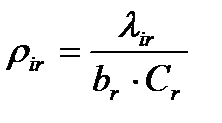(10.7) ;

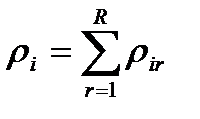(10.8)

Вероятность стационарного состояния сети P(n) определяется выражением: 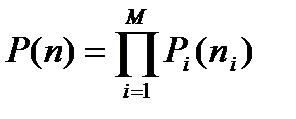, (10.9)

где n_i– число пакетов, передаваемых по i-ому каналу.

В формуле (10.9) при дисциплине обслуживания FCFSможно записать:

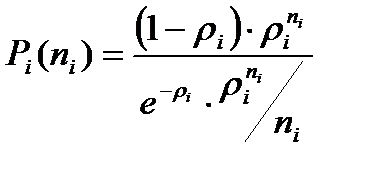(10.10)

P_i(n_i) - вероятность i-го состояния сети при числе пакетов, передаваемых по

i- ому каналу - n_i.

Предполагая, что передача пакетов по каналу осуществляется в соответствии с

дисциплиной FCFS, можно определить среднее количество пакетов в i- ом канале:

,

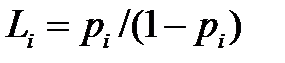тогда среднее число пакетов в сети в целом равно:

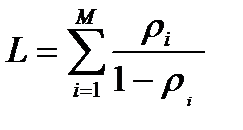(10.11)

В то же время, в соответствии с формулой Литтла среднее число пакетов в сети: L= ( Λ xT), где Т - среднее время пребывания пакета в сети.

Таким образом,

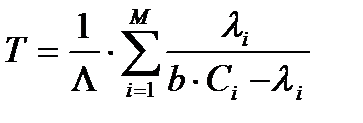(10.12)

Выражение (10.12) было впервые получено Клейнроком.

Различные методы квитирования и ограниченный объем буферной памяти узла коммутации, оказывает существенное влияние на характеристики базовой сети передачи данных,что должно находить отражение в соответствующих моделях СМО.

Рассмотрим модель гипотетической сети, в которой установлено семь УК (рисунок 10.1).

Рисунок 10.1 - Модель гипотетической сети

Рассмотрим процесс обмена информацией между УК₁ и УК₇. Между этими УК установлено 3 пути обмена пакетами, вероятность использования которых определяется величинами 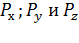. Очевидно, что сумма этих вероятностей:

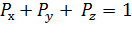
Допустим , что каждый УК обслуживает поступающий поток пакетов по дисциплине с ожиданием. Тогда интенсивность входящего потока можно обозначить

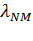, а интенсивность обработанного потока пакетов - 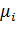. В соответствии с этими обозначениями рис. 10.1 будет иметь вид:

Рисунок 10.2 - Модель исследуемой сети

Допустим, что каждый УК может быть представлен моделью вида 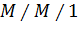, тогда время прибывания пакета в i-ом коммутаторе определяется по формуле:

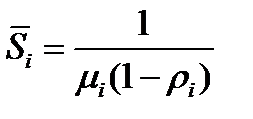(10.13)

В формуле (10.13) загрузка определяется отношением интенсивности входящего потока к интенсивности обслуженного потока. Например, для УК₃ загрузка определяется выражением: .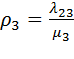

Средняя задержка пакета на маршруте, выбираемом с вероятностью 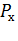, будет определяться выражением :

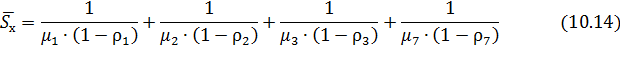
Тогда, с учетом соответствующих вероятностей 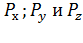, средняя задержка пакета в сети, представленной на рисунке (10.2), будет определяться выражением:

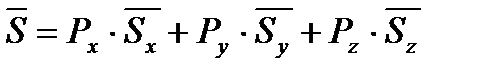(10.15)

РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА

Основная литература:

1. Степанов С.Н.Основы телетрафика мультисервисных сетей.- М.: Эко- Трендз, 2010.

2.Сутягин а Л.Н. Расчет межстанционных связей аналогово-цифровой ГТС/ Учебное пособие. ПГУТИ, 2010.

3. Гольдштейн Б.С., Соколов Н.А., Яновский Г.Г. Сети связи // СПб.: БХВ-2010.