I. Постановка задачи оптимальной линейной фильтрации. Методы оптимальной линейной фильтрации.

Постановка задачи оптимальной линейной фильтрации

Пусть наблюдается некоторый дискретный сигнал 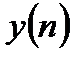, который линейным образом связан с полезным сигналом 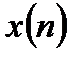уравнением наблюдения:

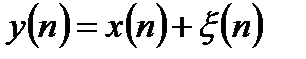, (1.1)

где 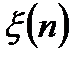- дискретный белый шум наблюдения.

Полезный дискретный сигнал в общем случае является случайным и задается некоторым разностным уравнением, одним из распространенных примеров которого является следующее:

, (1.2)

где 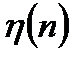- дискретный белый шум, формирующий полезный сигнал.

Дискретный фильтр оптимальной линейной фильтрации должен сформировать оценку полезного сигнала 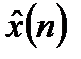, которая характеризуется минимальной ошибкой.

Методы оптимальной линейной фильтрации

Существуют следующие основные методы оптимальной линейной фильтрации:

- метод наименьших квадратов;

- метод реккурентной оптимальной линейной фильтрации.

В качестве критерия оптимальности обоих методов выбирается критерий минимума суммы квадратов наблюдаемых значений 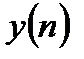от оцениваемых значений :

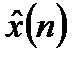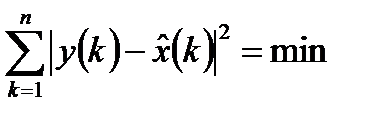. (1.3)

Если шум наблюдения являются гауссовским белым шумом, то оценка по критерию минимума совпадает с оценкой по методу максимума правдоподобия.

Отличие метода наименьших квадратов от реккурентной оптимальной фильтрации заключается в том, что формирование оптимальной оценки полезного сигнала осуществляется в нереальном масштабе времени после проведения всех измерений. Это приводит к следующим недостаткам метода МНК:

- большая емкость памяти устройств обработки;

- задержка выдачи оценки полезного сигнала.

От недостатков метода МНК свободны реккурентные алгоритмы оптимальной фильтрации, при которых вновь поступающий входной сигнал немедленно используется для уточнения ранее полученной оценки полезного сигнала:

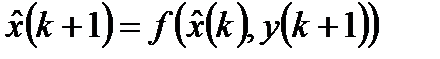. (1.4)

Согласно алгоритму (1.4) обработка входного сигнала происходит последовательно в реальном масштабе времени. Теория реккурентной оптимальной линейной дискретной фильтрации случайных гауссовских сигналов была разработана американскими учеными Р.Е. Калманом и Р.С. Бьюси в 1960 – 1961 гг. Иногда термин реккурентной оптимальной линейной дискретной фильтрации случайных деесовских сигналов заменяют оптимальной линейной фильтрацией Калмана.

В ряде простейших случаев реккурентный алгоритм оптимальной линейной фильтрации может быть получен путем математических преобразований алгоритмов, полученных методом МНК. В большинстве случаев необходимо использовать оригинальные уравнения реккурентной оптимальной фильтрации, частным случаев которых является фильтр Калмана.