Iii. Оптимальная линейная фильтрация полезного сигнала с постоянным приращением
Пусть разностное уравнение для неслучайного полезного сигнала имеет следующий вид:
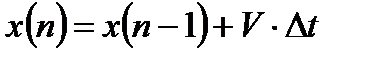 , (3.1)
, (3.1)
где 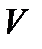 - скорость изменения сигнала;
- скорость изменения сигнала;
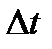 - интервал дискретизации.
- интервал дискретизации.
 Разностному уравнению соответствует модель полезного сигнала в виде следующего полинома первого порядка:
Разностному уравнению соответствует модель полезного сигнала в виде следующего полинома первого порядка:
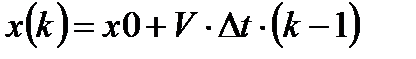 , (3.2)
, (3.2)
где 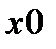 ,
, 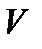 - некоторые параметры неслучайного полезного сигнала (начальное значение, скорость изменения).
- некоторые параметры неслучайного полезного сигнала (начальное значение, скорость изменения).
Оценивание методом МНК
Параметры 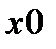 ,
, 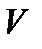 должны быть оценены по результатам измерений
должны быть оценены по результатам измерений 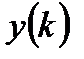 ,
, 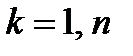 . В соответствии с методом МНК минимизируемый критерий в данном случае запишется следующим образом:
. В соответствии с методом МНК минимизируемый критерий в данном случае запишется следующим образом:
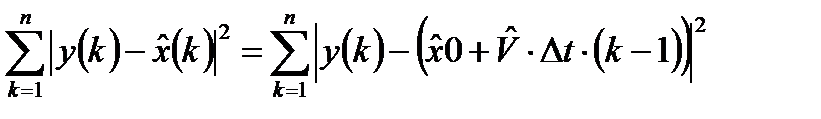 . (3.3)
. (3.3)
В качестве оценок МНК будем использовать те значения параметров модели полезного сигнала 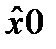 и
и 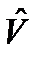 , для которых записанный критерий оптимальности принимает минимальное значение или производные критерия оптимальности равны нулю:
, для которых записанный критерий оптимальности принимает минимальное значение или производные критерия оптимальности равны нулю:
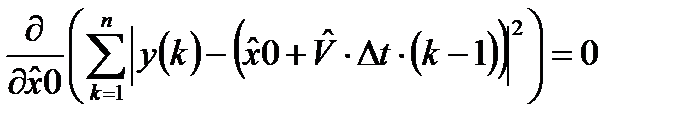 ; (3.4)
; (3.4)
 . (3.5)
. (3.5)
В результате применения операции дифференцирования по оцениваемым параметрам получим:
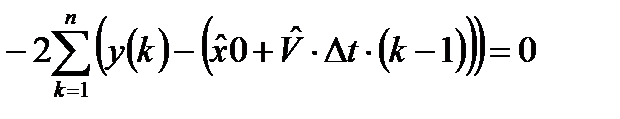 ;
;
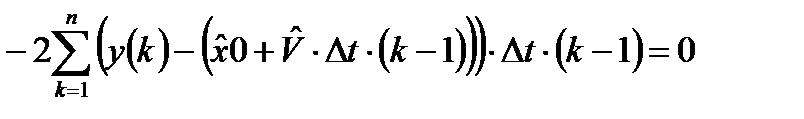 .
.
После выполнения операции суммирования с точностью до несущественных постоянных множителей получим:
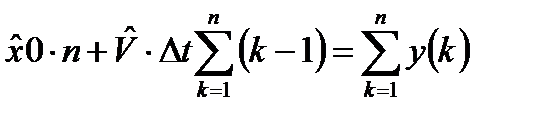 ;
;
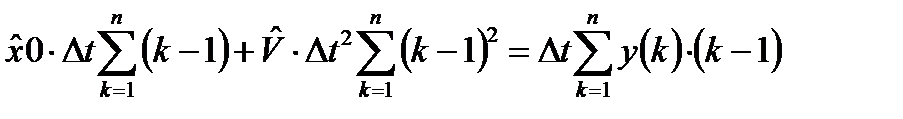 .
.
Таким образом, получена система двух линейных уравнений относительно искомых параметров 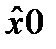 и
и 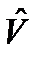 . Решение системы имеет следующий вид:
. Решение системы имеет следующий вид:
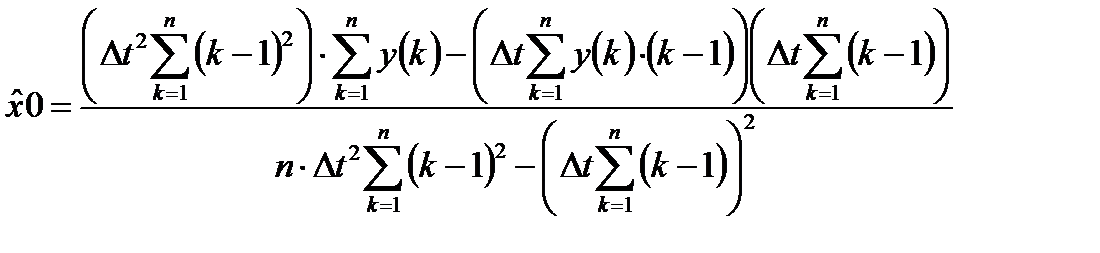 ;
;
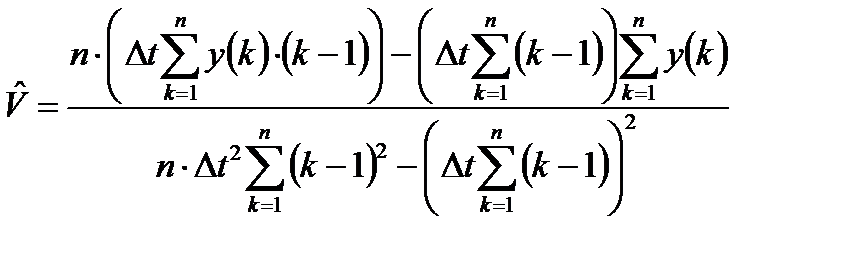 .
.
Учтем следующие выражения:
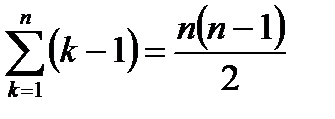 ;
; 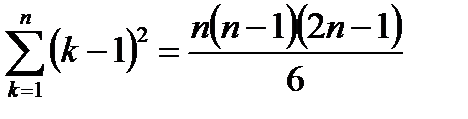 .
.
В этом случае оптимальные оценки параметров полезного сигнала методом МНК примут следующий окончательный вид:
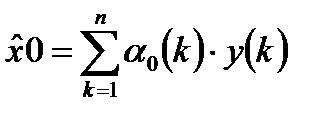 ; (3.6)
; (3.6)
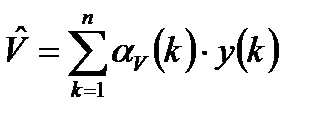 , (3.7)
, (3.7)
где 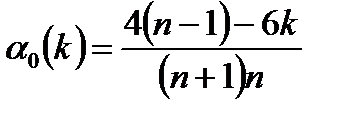 ;
;
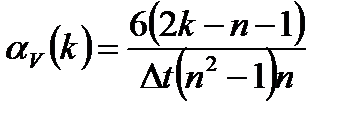 .
.
Соответственно, оценка сигнала на момент последнего измерения запишется следующим образом:
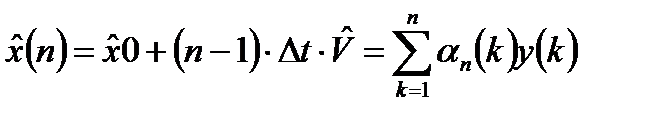 , (3.8)
, (3.8)
где 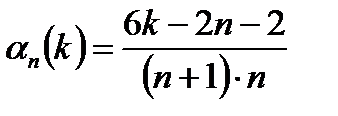 .
.
Экстраполированное значение оценки сигнала на один дискрет времени вперед определяется выражением:
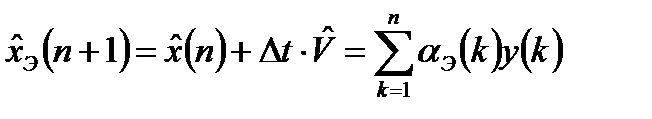 , (3.9)
, (3.9)
где 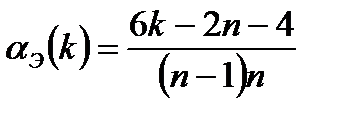 .
.
Дисперсии полученных оценок скорости 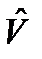 , фильтрованного
, фильтрованного 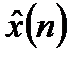 и экстраполированного
и экстраполированного 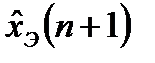 сигналов с учетом некоррелированности шумов наблюдения
сигналов с учетом некоррелированности шумов наблюдения 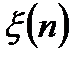 в различных дискретах времени запишутся в виде:
в различных дискретах времени запишутся в виде:
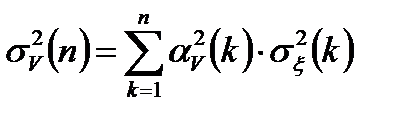 ,
,
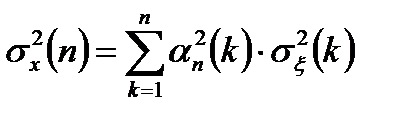 , (3.10)
, (3.10)
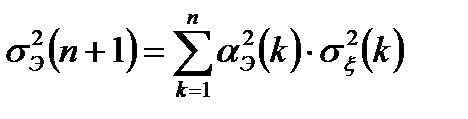 .
.
Оценивание методом рекуррентной фильтрации
Рекуррентные уравнения оптимальной фильтрации могут быть получены в результате взвешенного суммирования экстраполированного значения оцениваемого сигнала с текущим рассогласованием:
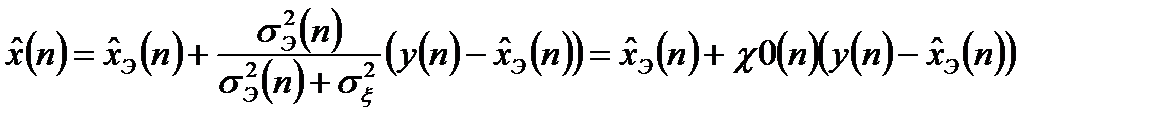 , (3.11)
, (3.11)
где 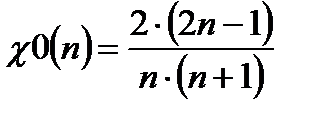 - коэффициент фильтрации по положению сигнала.
- коэффициент фильтрации по положению сигнала.
Вес текущего рассогласования 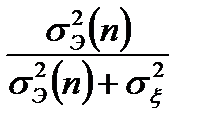 стремится к нулю, если экстраполированная оценка является идеальной (
стремится к нулю, если экстраполированная оценка является идеальной (  ), и стремится к единице, если дееальным является текущий входной сигнал (
), и стремится к единице, если дееальным является текущий входной сигнал (  ). В последнем случае выражение (3.11) принимает вырожденный вид:
). В последнем случае выражение (3.11) принимает вырожденный вид: 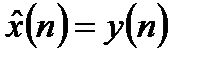 .
.
Результирующие уравнения оптимальной дискретной линейной фильтрации имеют следующий рекуррентный вид:
 , (3.12)
, (3.12)
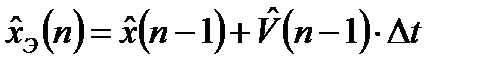 , (3.13)
, (3.13)
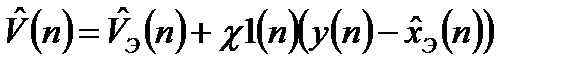 , (3.14)
, (3.14)
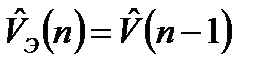 , (3.15)
, (3.15)
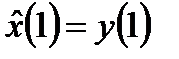 ,
,
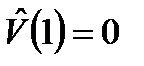 ,
,
где 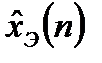 - экстраполированное значение измеряемого дискретного сигнала;
- экстраполированное значение измеряемого дискретного сигнала;
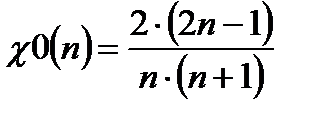 - коэффициент фильтрации по положению сигнала;
- коэффициент фильтрации по положению сигнала;
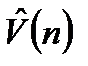 - измеренное значение скорости изменения дискретного сигнала;
- измеренное значение скорости изменения дискретного сигнала;
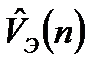 - экстраполированное значение скорости изменения дискретного сигнала;
- экстраполированное значение скорости изменения дискретного сигнала;
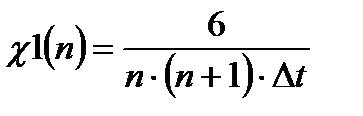 - коэффициент фильтрации по скорости сигнала.
- коэффициент фильтрации по скорости сигнала.
Структурная схема оптимального линейного дискретного фильтра сигнала с постоянным приращением имеет следующий вид: рисунок 3.1.
В соответствии с рисунком 3.1 фильтр для фильтрации сигнала с постоянным приращением представляет собой дискретную следящую систему с двумя цифровыми интеграторами в разомкнутой цепи, измерением скорости приращения и переменными коэффициентами фильтрации контуров по положению и скорости.
По причине неслучайного сигнала коэффициенты фильтрации стремятся к нулю с течением времени, что приводит к размыканию обратных связей и накоплению ошибок, вызванных конечной разрядностью представления чисел. Этот недостаток устраняется использованием квазиоптимальных алгоритмов 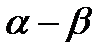 - фильтрации, для которых коэффициенты фильтрации не меняются во времени, а ошибка фильтрации минимизируется не для каждого отсчета, а только после окончания переходного процесса.
- фильтрации, для которых коэффициенты фильтрации не меняются во времени, а ошибка фильтрации минимизируется не для каждого отсчета, а только после окончания переходного процесса.
Рисунок 3.1 – структурная схема реккурентной оптимальной линейной фильтрации сигнала с постоянным приращением
Дата добавления: 2017-09-19; просмотров: 1008;
