Iv. Уравнения фильтра Калмана

Пусть наблюдается некоторый дискретный сигнал 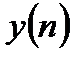, который линейным образом связан с полезным сигналом 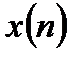уравнением наблюдения:

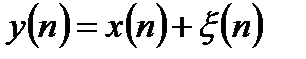, (4.1)

где 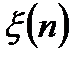- дискретный белый шум наблюдения.

Разностное уравнение для случайногополезного сигнала имеет следующий вид:

, (4.2)

где 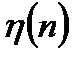- дискретный белый шум.

В этом случае невозможно получить уравнения оптимальной фильтрации путем математических преобразований уравнений фильтрации, полученных методом МНК и необходимо использовать уравнения фильтра Калмана. Уравнения фильтра Калмана совпадают с алгоритмами фильтрации неслучайного постоянного сигнала:

, (4.3)

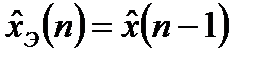. (4.4)

Однако коэффициент фильтрации в этом случае отличается и описывается следующим рекуррентным выражением, полученным Калманом:

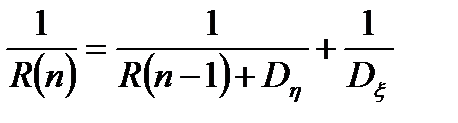, (4.5)

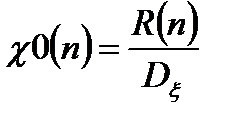, (4.6)

где 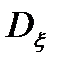и 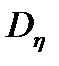- дисперсии дискретных случайных процессов шума наблюдения 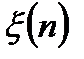и формирующего шума .

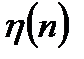Вывод уравнений Калмана приводится в следующем источнике: Васильев К.К. Методы обработки сигналов: Учебное пособие. – Ульяновск, 2001. – 80 с. (с. 47).

Квазиоптимальная рекуррентная линейная дискретная фильтрация