Синтез цифровой следящей системы для прототипа с первым порядком астатизма

Будем полагать, что передаточная функция разомкнутой аналоговой следящей системы содержит один интегратор:

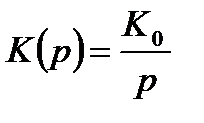. (3.1)

Передаточная функция замкнутой следящей системы имеет следующий вид:

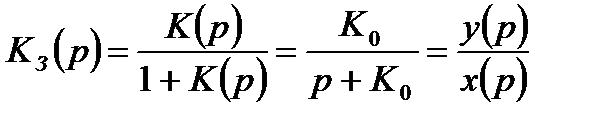. (3.2)

Характеристический полином следящей системы запишется следующим образом:

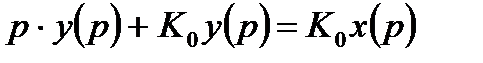(3.3)

или

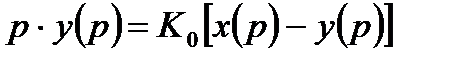. (3.4)

Дифференциальное уравнение, описывающее работу следящей системы в соответствии с выражением (3.4) примет вид:

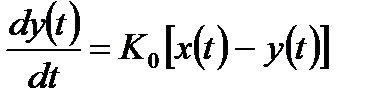. (3.5)

Переход от дифференциального уравнения к разностному уравнению осуществляется следующим образом:

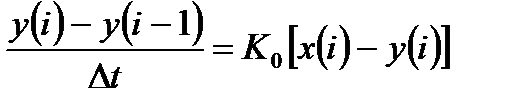. (3.6)

Для получения реккурентного вида разностного уравнения выразим текущее значение выходного сигнала 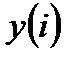через его предыдущие значения:

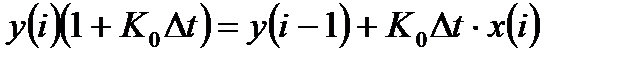
или

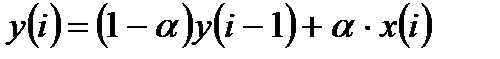, (3.7)

где .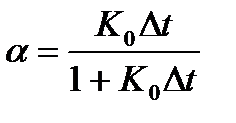

Преобразуем полученный реккурентный алгоритм к виду, содержащему формирование экстраполированного значения выходного сигнала и рассогласования между входным сигналом и экстраполированным значением выходного сигнала:

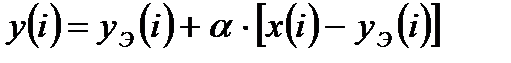, (3.8)

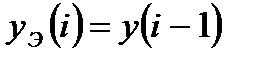. (3.9)

Полученный алгоритм цифровой фильтрации также называется 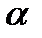- фильтром. Коэффициент фильтрации 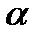может быть получен пересчетом коэффициента преобразования 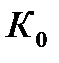разомкнутой аналоговой следящей системы с учетом интервала дискретизации 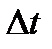. Алгоритму соответствует структурная схема, приведенная на рисунке 3.1.

Рисунок 3.1 – структурная схема 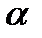- фильтра