Методика синтеза квазиоптимальных рекуррентных линейных дискретных фильтров

Пусть задана некоторая аналоговая следящая система, эквивалентная структурная схема которой имеет следующий вид: рисунок 2.1.

Рисунок 2.1 – эквивалентная структурная схема аналогового прототипа цифровой следящей системы

Предполагается, что известна передаточная функция 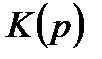разомкнутой следящей системы аналогового прототипа. Наиболее распространены следующие типы передаточных функций, соответствующие следящим системам с первым и вторым порядками астатизма:

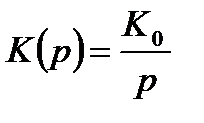, (2.1)

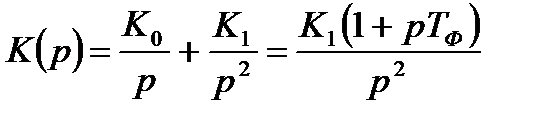. (2.2)

Синтез цифровой следящей системы по аналоговому прототипу будет проводиться методом замены производных конечными разностями:

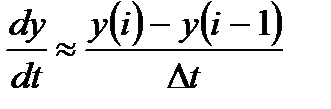, (2.3)

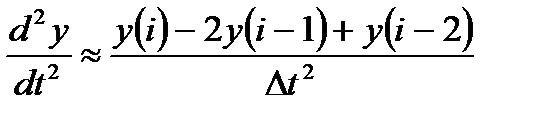. (2.4)

Методика синтеза подробно разработана и применена для следящих систем с 1-ым, 2-ым и 3-им порядком астатизма белорусским ученым, профессором, доктором технических наук А.Е. Охрименко и включает в себя следующие этапы:

1) Определение передаточной функции замкнутой следящей системы в соответствии с выражением:

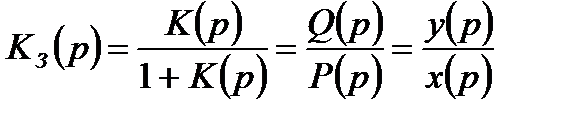. (2.5)

2) Запись характеристического полинома следящей системы в следующем виде:

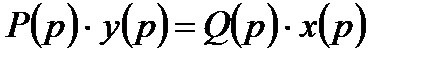. (2.6)

3) Определение по характеристическому полиному дифференциального уравнения, описывающего работу следящей системы.

4) Получение разностного уравнения цифровой следящей системы путем замены в полученном дифференциальном уравнении производных конечными разностями.

5) Преобразование полученного разностного уравнения к рекуррентному виду, связывающему текущее значение выходного сигнала с его предыдущими значениями и значениями входного сигнала.

6) Преобразование полученного рекуррентного алгоритма к виду, содержащему дискриминатор сигнала ошибки, цепи цифровой фильтрации и формирования экстраполированного значения выходного сигнала.