SDC-параметризация нелинейных объектов

Пусть нелинейный управляемый объект описывается векторным дифференциальным уравнением

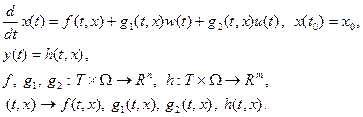(2.40)

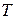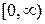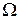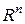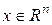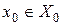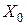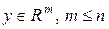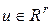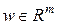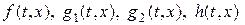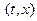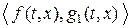Здесь − интервал ; −область (открытое связанное множество) , содержащая начало; −состояние системы; , − область возможных начальных состояний системы; − выход системы; −управление, подлежащее нахождению; −неизвестное возмущение; матрицы действительны и непрерывны. Предполагается, что при вех пары и 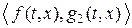являются управляемыми, пара 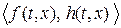наблюдаемой. Кроме того, функции 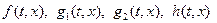будем предполагать достаточно гладкими, чтобы через любые 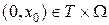проходило одно и только одно решение (2.40) 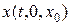и был бы единственный соответствующий выход системы .

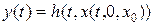Представим систему (2.40) в несколько ином, эквивалентном виде. Для этого используем метод SDC-параметризации (State Dependent Coefficient, [39]).

Предположение 2.5.1.Вектор-функция 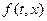─ непрерывная дифференцируемая по 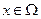, т.е. 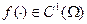и .

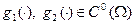Предположение 2.5.2.Без потери общности положим, что условие 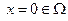есть точка равновесия системы при 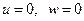так, что 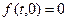и .

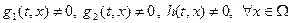Предположение 2.5.3.Положим [16], что

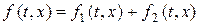, (2.41)

где 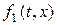− нелинейность низкого порядка, т.е.

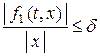, − малая величина,

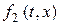− нелинейность высшего порядка, т.е.

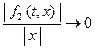при .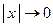

Учитывая предположения, сделанные относительно свойства рассматриваемых нелинейностей, перейдем от (2.41) к

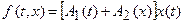. (2.42)

Предположим также, что

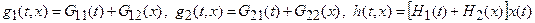. (2.43)

Такие представления в литературе, относящейся к теории автоматического управления, называют по-разному: кажущейся линеаризацией (apparent linearization [46]), расширенной (экстенсивной) линеаризацией (extended linearization [28]) и, значительно позже, представлением в виде системы с параметрами, зависящими от состояния (State-Dependent-Coefficient factorization [24]).

Таким образом, нелинейная система (2.40) может быть преобразована в 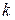эквивалентных систем относительно исходной, но не эквивалентных относительно друг друга, с параметрами, зависящими от состояния (SDC)

(2.44)

Представление системы (2.40), если 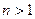, в виде (2.44) не является единственным [43]. Пусть количество возможных представлений этой нелинейности в виде (2.44), которые при заданных начальных условиях не обращаются в бесконечность, есть .

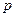Отметим, что успех выполнения задачи управления исходной нелинейной системой с использованием ее SDC-модели напрямую зависит от структурных свойств полученного преобразования. А именно, от управляемости и наблюдаемости SDC-модели. Другими словами, представление системы в виде управляемой и наблюдаемой SDC-модели гарантирует существование решение задачи управления. Вопрос построения управляемой и наблюдаемой SDC-модели рассматривается при постановке задачи управления в разделе 2.7.

Определение 2.5.1.Представление системы (2.40) в виде (2.44) является эквивалентным, если матрицы 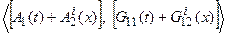и 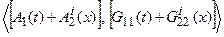образуют управляемые пары, а матрицы 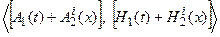образуют наблюдаемую пару при всех возможных 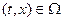, , 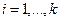где 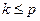количество возможных представлений вида (2.44), при которых сохраняется свойство управляемости и наблюдаемости исходной системы.

Для скалярных систем параметризация SDC уникальна для всех 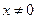, т.е.

.

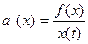Рассмотрим систему нелинейную систему вида (2.40), состояние которой 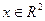, т.е. 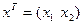. В этом простом случае возможны, по крайней мере, два варианта параметризации. Действительно, предположим, что вектор 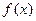нелинеен только по переменной , тогда 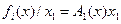. Если же вектор 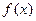нелинеен только по переменной 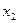, тогда 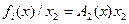. Предположим, что матрицы 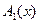и 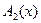таковы, что 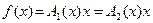. Тогда

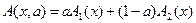(2.45)

является параметризацией SDC для любого 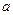, что легко проверить, умножив обе стороны на 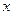. Поэтому, матрица представляет бесконечное семейство SDC параметризации.

Групповая параметризация SDC для многовариантных систем создаёт дополнительные степени свободы. Матрица может быть представлена параметрически как гиперповерхность, содержащая 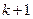отличных результатов параметризации (если они существуют) и 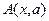будет определяться следующим выражением

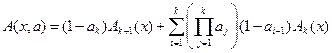
где 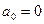[34].

Отметим, что если гиперповерхность параметризации удалось сформировать в виде , то, очевидно, параметры синтезированного оптимального регулятора будут зависеть от параметра 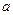, т.е. 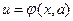. Таким образом, параметризация нелинейного вектора 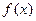в виде 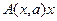при синтезе регулятора гипотетически представляет разработчикам дополнительные возможности для получения тех или иных желаемых результатов функционирования системы с нелинейной обратной связью.