II. Виды средних величин и методы их расчета.
На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.

А. Степенные средние (простые и взвешенные)
От того в каком виде представлены исходные данные для расчета средней, зависит каким образом будет реализовано ее исходное соотношение (ИСС). В каждом конкретном случае для реализации ИСС потребуется один из видов средней величины: средняя арифметическая, средняя гармоническая, средняя геометрическая или средняя квадратическая.
Различные средние выводят в общей формулы средней степенной (при различной величине k)
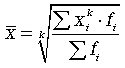
при k = - 1 – средняя гармоническая;
k = 0 – средняя геометрическая;
k = 1 – средняя арифметическая;
k = 2 – средняя квадратическая.
K = 3 – средняя кубическая
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
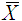 =
= 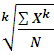
Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем, каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весомили весом средней.
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
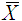 =
= 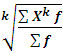
Дата добавления: 2017-04-20; просмотров: 1336;
