I. Основные параметры несинусоидальных величин.

На практике в большинстве случаев кривые ЭДС и токов отличны от синусоиды.

Несинусоидальными являются ЭДС, создаваемые генераторами периодических импульсов (пилообразных, ступенчатых и др.).

В электрических цепях, содержащих нелинейные R, L или C, даже при синусоидальной ЭДС возникают несинусоидальные токи и напряжения. Расчет таких электрических цепей можно упростить, если воспользоваться методами расчета при синусоидальной ЭДС.

При расчете пользуются разложением периодических несинусоидальных функций в тригонометрический ряд (ряд Фурье или гармонический ряд)

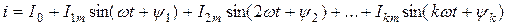
I₀ – постоянная составляющая (постоянный ток) – нулевая гармоника.

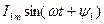- основная волна – первая гармоника, частота колебаний этой гармоники совпадает с частотой несинусоидального тока.

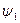- начальная фаза – зависит от начала отсчета времени.

I_1m – амплитуда гармоники.

Все остальные составляющие – это высшие гармоники (k>1).

– основная частота, угловая скорость первой гармоники.

T – период несинусоидальной периодической кривой, равной периоду первой гармоники.

Следовательно, несинусоидальный ток можно рассматривать как складывающийся из постоянного тока и переменных синусоидальных токов различной частоты и с различными начальными фазами.

Если функция задается графиком, то она может быть представлена конечным рядом (3-7 членов ряда).

Существует много способов графического решения, в том числе использование специальных шаблонов.

Разложение несинусоидальной периодической функции на ряд гармонических сводится к определению амплитуд и начальных фаз каждой гармоники.

Несинусоидальная периодическая функция характеризуется тремя значениями:

- максимальным;

- действующим;

- средним.

Для каждой гармоники эти значения определяются так же, как и при рассмотрении электрических цепей синусоидального тока.

Действующее значение несинусоидальной величины зависит только от действующего значения ее гармоник и не зависит от их фаз.

Действующее значение измеряется с помощью электрических приборов:

- электромагнитных;

- электростатических;

- электродинамических.

Среднее значение несинусоидальной величины за период равно постоянной составляющей, так как суммарная площадь, ограниченная кривой, за период любой гармонической составляющей равна 0.

I_ср = I₀, U_ср = U₀, E_ср = E₀.

Амплитудное (максимальное) значение гармонических составляющих уменьшается с увеличением номера гармоники. Поэтому часто при анализе электрических цепей несинусоидального тока ограничиваются первыми членами ряда.

Сравнивать несинусоидальные величины удобно по коэффициентам.

характеризуют форму кривой (отличие от синусоиды)

- коэффициент искажения – показатель качества электрической энергии энергосистемы

- коэффициент пульсации – характеризует преобразование синусоидального тока в постоянный.

II. Расчет электрической цепи с несинусоидальными ЭДС и токами.

Применяют метод наложения, при котором считается, что линейная электрическая цепь для каждой гармонической составляющей ЭДС независима. Метод состоит из трех этапов:

1) разложение действующей в цепи ЭДС на гармонические составляющие;

2) расчет токов и напряжений для каждой составляющей ЭДС;

3) суммирование решений, полученных для каждой составляющей.

Пример. Если в цепи действует ЭДС:

,

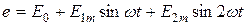то она аналогична действию трех последовательно соединенных ЭДС E₀, E₁ и E₂. Мгновенное значение тока цепи будет равно

i = i₀ + i₁ + i₂.

При расчете следует учитывать, что емкостное сопротивление с увеличением порядка гармоники уменьшается в k раз:

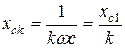
индуктивное сопротивление – в k раз увеличивается:

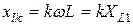
активное сопротивление – возрастает (за счет поверхностного эффекта), но незначительно. При низких частотах можно принять

R_k = R₁

– сопротивление постоянному току. Эти свойства реактивных элементов (L – задерживать токи высоких частот, C – задерживать токи низких частот, не пропускать постоянную составляющую I₀) используются в электрических фильтрах. Принцип действия основан на зависимости эквивалентного сопротивления Z_э от частоты.

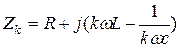- полное сопротивление цепи для любой гармоники.

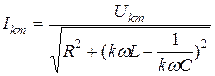- амплитудное значение тока для k гармоники.

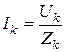- действительное значение тока для k гармоники.

Зная действительные значения токов каждой гармоники, можно определить активную мощность цепи:

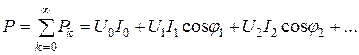
S=UI – полная мощность несинусоидального тока,

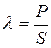– коэффициент мощности (при наличии высших гармоник).