Действительный ток в цепи в переходном процессе
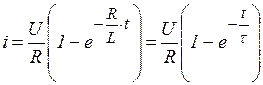 (5.7)
(5.7)
На рис. 5.2 изображена кривая изменения тока в рассматриваемой цепи. Скорость протекания переходного процесса определяется постоянной времени цепи
 |
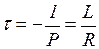 (5.8)
(5.8)
Рис. 5.2
Постоянная времени 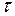 графически определяется длиной касательной
графически определяется длиной касательной 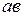 (рис. 5.2) и кривой
(рис. 5.2) и кривой 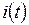 . Значения тока
. Значения тока 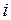 в цепи различных моментов времени определяются из формулы (5.7) и приведены в таблице 5.1
в цепи различных моментов времени определяются из формулы (5.7) и приведены в таблице 5.1
Таблица 5.1
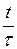
| ||||
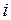
|
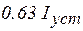
|
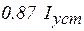
|
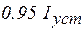
|
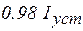
|
(рис.5.5)
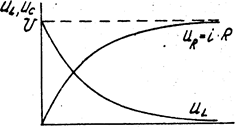
Напряжение на индуктивном элементе в переходный период (рис. 5.3)
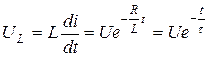 (5.9)
(5.9)
Характер изменения величин в цепях с одним накопителем энергии подчиняется экспоненциальному закону. Таким образом, задача сводится к определению конкретных значений начальных и остановившихся токов и напряжений.
Пример 5.1. По какому закону будут изменяться токи 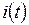 ,
, 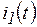 ,
, 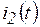 и напряжение
и напряжение 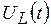 цепи на рис. 5.4 при переходном процессе, вызванном замыканием рубильника?
цепи на рис. 5.4 при переходном процессе, вызванном замыканием рубильника?
Решение сводится к определению начальных и установившихся значений токов и напряжений. Так как ток в катушке индуктивности скачком изменяться не может (см. формулу (5.2)), схема для определения начальных значений величин примет вид, изображенный на рис. 5.5, где
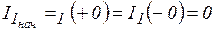
Остальные токи, напряжения в схеме определяются как обычно для цепей постоянного тока: 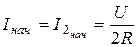 ;
; 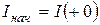 ;
; 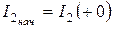 ;
;
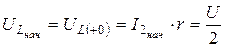
 Схема на рис. 5.6 для установившегося режима получена при
Схема на рис. 5.6 для установившегося режима получена при 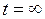 , а
, а 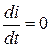 и
и 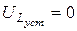


Рис.5.4 Рис. 5.5 Рис. 5.6
Кривые изменения токов и напряжений изображены на рис. 5.7 и рис. 5.8.
Отключение цепи с 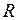 и
и 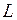 от источника постоянного напряжения. При отключении индуктивной катушки от источника (рис.5.9) ток в ней
от источника постоянного напряжения. При отключении индуктивной катушки от источника (рис.5.9) ток в ней 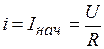 в первый момент времени остается неизменным, зато в резисторе
в первый момент времени остается неизменным, зато в резисторе 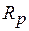 ток
ток 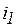 меняется скачком от нудя до -
меняется скачком от нудя до - 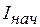 (знак минус показывает, что он направлен против указанного на схеме положительного направления). Для уменьшения потерь в цепи при включенной катушке последовательно с разрядным сопротивление включен диод Д, благодаря чему ток
(знак минус показывает, что он направлен против указанного на схеме положительного направления). Для уменьшения потерь в цепи при включенной катушке последовательно с разрядным сопротивление включен диод Д, благодаря чему ток 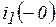 до размыкания выключателя равен нулю.
до размыкания выключателя равен нулю.
Согласно второму закону Кирхгофа, 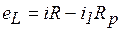 ; так как
; так как 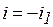 , то
, то
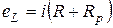 или
или 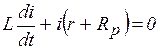
Отсутствие правой части в уравнении означает, что ток в переходном процессе равен свободной составляющей (энергия извне не поступает) 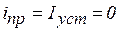
Ток в цепи 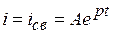
Поскольку 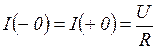 , то
, то 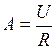 .
.
Таким образом, 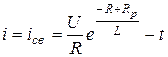 ток в разрядном сопротивлении
ток в разрядном сопротивлении 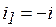 (рис. 5.10).
(рис. 5.10).
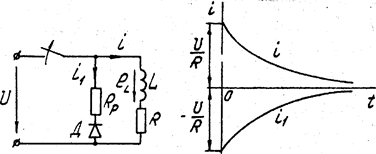
Рис. 5.9 Рис. 5.10
Включение цепи с 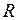 и
и 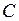 на постоянное напряжение. Для цепи (рис. 5.11) по второму закону Кирхгофа
на постоянное напряжение. Для цепи (рис. 5.11) по второму закону Кирхгофа 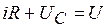 ; так как
; так как 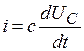 , получаем уравнение
, получаем уравнение
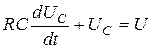
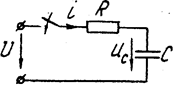
Рис. 5.11
Напряжение на конденсаторе в процессе заряда (рис. 5.12)
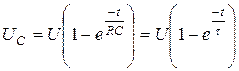 (5.14)
(5.14)
Ток в цепи заряда конденсатора
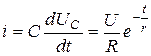 (5.15)
(5.15)
где 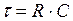 .
.
Пример 5.2. Определить начальные и установившиеся значения токов 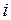 ,
, 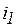 ,
, 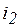 , и напряжений
, и напряжений 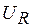 ,
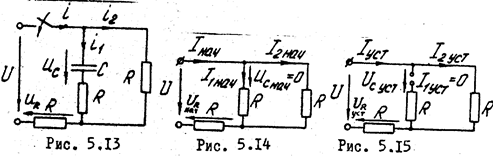
, 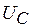 в цепи, изображенной на рис. 5.13, при замыкании ключа.
в цепи, изображенной на рис. 5.13, при замыкании ключа.
Решение. Схема для определения начальных стечении величин при 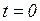 изображена на рис. 5.14, где
изображена на рис. 5.14, где 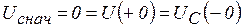 ,
,
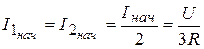
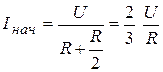 ,
, 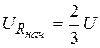
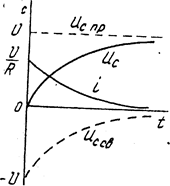
Рис. 5.12
Схема для определения установившихся значений величин при 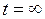 приведена не рис. 5.15.
приведена не рис. 5.15.
Известно, что постоянный ток через емкость в установившемся процессе не проходит: 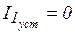 ,
, 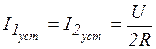 ,
, 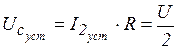 ,
, 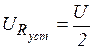
Разряд конденсатора на сопротивление 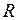 . Уравнение для цепи (рис. 5.16), составленное по второму закону Кирхгофа, имеет вид
. Уравнение для цепи (рис. 5.16), составленное по второму закону Кирхгофа, имеет вид 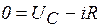 , где
, где 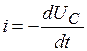 - знак минус означает, что направление тока при разряде конденсатора не совпадает с положительным направлением напряжения
- знак минус означает, что направление тока при разряде конденсатора не совпадает с положительным направлением напряжения 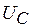 . В конце процесса
. В конце процесса 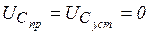 . Поэтому
. Поэтому 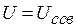 ,
, 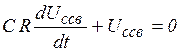
Дата добавления: 2019-02-07; просмотров: 730;
