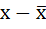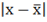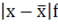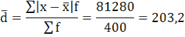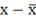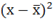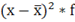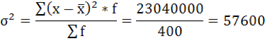Статистические показатели: абсолютные, относительные, средние, вариации.
Показатели вариации в статистике. Вариация. Абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение Способы расчета дисперсии. Относительные показатели вариации: коэффициенты осцилляции, вариации. Структурные характеристики вариационного ряда распределения. Анализ структуры вариационных рядов распределения.
______________________________________________________________
Вспомним ранее пройденное:

Вариация - это различия в значениях какого-либо признака у разных единиц изучаемой совокупности в один и тот же период (момент) времени.
Причиной вариации бывают разные условия существования разных единиц совокупности. Например, даже близнецы в процессе жизни приобретают различия в росте, весе, а также в таких признаках, как уровень образования, доход, количество детей и т.д.
Вариация возникает в результате того, что сами значения признака складываются под суммарным влиянием разнообразных условий, которые разным образом сочетаются в каждом отдельном случае. Таким образом, величина любого варианта объективна.
Вариация характерна всем без исключения явлениям природы и общества, кроме законодательно закрепленных нормативных значений отдельных социальных признаков (например, ГОСТ). Исследования вариации в статистике имеют огромное значение, помогают познать сущность изучаемого явления. Нахождение вариации, выяснение ее причин, выявление влияния отдельных фактов дают важную информацию для внедрения научно обоснованных управленческих решений.
Средняя величина дает обобщенную характеристику признака совокупности, но она не раскрывает ее строения. Среднее значение не показывает, как располагаются вокруг нее варианты осредненного признака, распределены ли они вблизи средней или отклоняются от нее. Средняя в двух совокупностях может быть одинаковой, но в одном варианте все индивидуальные значения отличаются от нее незначительно, а в другом – эти отличия велики, т.е. в первом случае вариация признака мала, а во втором – велика, это имеет очень важное значение для характеристики значимости средней величины.
Для того, чтобы руководитель организации, управляющий, научный сотрудник могли изучать вариацию и управлять ей, статистикой разработаны специальные методы исследования вариации (система показателей). С их помощью вариация находится, характеризуются ее свойства.

| Показатель | Обозначение | Характеристика показателя | Формула | Пример расчета | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Размах вариации | R | это разность между максимальным и минимальным значениями признака. Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности. | R = Xmax-Xmin | Пример 1 (для простых показателей вариации). Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. Размах вариации = 9 - 2 = 7 лет. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Среднее линейное отклонение | 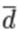
| это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней. Среднее линейное отклонение показывает, на сколько в среднем каждое значение признака отклоняется от средней величины. Эта величина всегда именованная и измеряется в тех же величинах, в которых даны статистические показатели. Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признаков совокупности. Средние линейные отклонения применяются на практике для анализа состава рабочих, ритмичности производства, равномерности поставок материалов и т.д. | Простое - для несгруппированных данных (ранжировочного ряда)
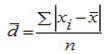
| Пример 1. Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
В нашем примере: 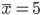 лет = (2+3+4+7+9) : 5 лет = (2+3+4+7+9) : 5
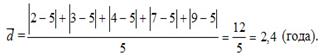
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Взвешенное - для вариационного интервального ряда:
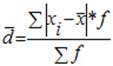
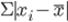 – сумма абсолютных значений (модулей) отклонения варианта от средней арифметической;
f – частота. – сумма абсолютных значений (модулей) отклонения варианта от средней арифметической;
f – частота.
| Пример 2 (для взвешенных показателей вариации). По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Удобно пользоваться таблицей расчётных данных:
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дисперсия. | σ2 | представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. | Дисперсия простая:
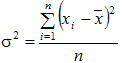
| Пример 1. Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. 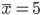 лет = (2+3+4+7+9) : 5 лет = (2+3+4+7+9) : 5
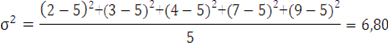
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Дисперсия взвешенная:
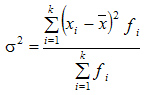
| Из примера 2. Расчёты оформим в таблицу:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Среднее квадратичное отклонение | σ | равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической (квадрату из значения дисперсии). Среднее квадратическое отклонение дает обобщенную характеристику признака совокупности и показывает во сколько раз в среднем колеблется величина признака совокупности. В зарубежной литературе оно называется стандартным отклонением и применяется в различных стандартах. Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения. Среднее квадратическое отклонение является мерой надежности средней величины: чем оно меньше, тем точнее средняя арифметическая. | Простое - для несгруппированных данных (ранжировочного ряда):
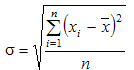 или
σ =
или
σ = 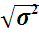
| Пример 1. Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.  лет = (2+3+4+7+9) : 5 лет = (2+3+4+7+9) : 5
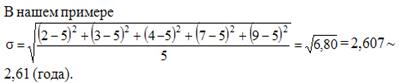
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Взвешенное - для вариационного интервального ряда:
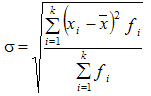
| Из примера 2.
σ = 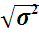
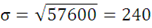 руб. руб.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент вариации | V | это отношение среднеквадратического отклонения к среднеарифметическому, рассчитывается в процентах. Коэффициент вариации позволяет судить об однородности совокупности: – < 17% – абсолютно однородная; – 17–33%% – достаточно однородная; – 35–40%% – недостаточно однородная; – 40–60%% – это говорит о большой колеблемости совокупности. | 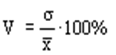
| Пример 1.V = 2,61/5 ×100% = 52,2 % Коэффициент вариации в данном примере говорит о большой колеблемости совокупности. | |||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2.Средний размер вклада в Сбербанке города будет равен 780 рублей (по средней взвешенной)
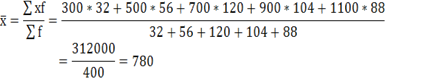 Тогда, коэффициент вариации равен:
V = 240/780 × 100% = 30,7%, т.е совокупность достаточно однородна.
Тогда, коэффициент вариации равен:
V = 240/780 × 100% = 30,7%, т.е совокупность достаточно однородна.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент осцилляции | VR | отношение размаха вариации к средней, в процентах. Отражает относительную колеблемость крайних значений признака вокруг средней. | 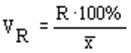
| Пример 1. VR = 7/ 5 × 100 % = 140 % | |||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2.Определим размах вариации как разность между наибольшим и наименьшим значением признака:
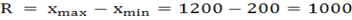 руб.
Тогда, VR = 1000/780 × 100 % = 128,2% руб.
Тогда, VR = 1000/780 × 100 % = 128,2%
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Линейный коэффициент вариации (относительное линейное отклонение). | V 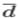
| характеризует долю усредненного значения абсолютного отклонения от средней величины. | 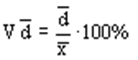
| Пример 1. V 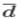 = 2,4/5 × 100% = 48% = 2,4/5 × 100% = 48%
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2. V 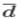 = 203,2/ 780 × 100% = 26,1% = 203,2/ 780 × 100% = 26,1%
|
В статистике проводят анализ структуры вариационных рядов распределения.
Основная задача их анализа – определение структуры, однородности совокупности, выявление характера и закономерности распределения. При статистическом анализе вариационных рядов распределения рассчитываются следующие его основные показатели:
1. Частость (W) – доля (удельный вес) отдельных групп в общей численности статистической совокупности. Частость представляет собой относительную величину структуры:
2. Накопленная частота (S) в ранжированном вариационном ряду показывает, сколько единиц совокупности имеют значение признака не больше (не меньше) заданного.
3. Накопленная частость ( Q) в ранжированном вариационном ряду показывает долю (удельный вес) единиц совокупности, имеющих значение признака не больше (не меньше) заданного.
4. Мода (Mo) – значение признака, которое чаще всего встречается в исследуемой статистической совокупности.
5. Медиана (Me) – значение признака у серединной единицы ранжированного вариационного ряда. Медиана делит вариационный ряд на две равные по числу единиц части.
Дата добавления: 2017-04-20; просмотров: 1768;