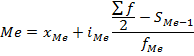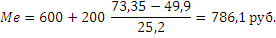Б. Структурные средние: мода, медиана.
Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.
Определение моды:
1) по несгруппированным данным.
Девять торговых фирм реализуют товар А по следующим ценам (тыс. руб.): 4,4; 4,3; 4,4; 4,5; 4,3; 4,3; 4,6; 4,2; 4,6. Наиболее часто встречается цена 4,3 тыс. руб. – она и является модальной (модой).
2) по сгруппированным данным:
- по дискретным рядам:
 Представим распределение торговых организаций города по уровню розничных цена на товар А. Представим распределение торговых организаций города по уровню розничных цена на товар А.
И таблицы видно, что наиболее распространенной является цена 55 руб., т.к. она наиболее часто встречается (в 60 организациях), поэтому цена 55 руб. является модальной (модой). - по интервальным рядам мода определяется по формуле:
где Мо – мода, x0 – значение начала модального интервала, h – размер модального интервала, fМо – частота модального интервала, fМо-1 – частота интервала, находящего перед модальным, fМо1 – частота интервала, находящего после модального.
Пример:
среднедушевых денежных доходов в 1998 г.
Интервал 400-600 в данном распределении будет модальным, т.к. имеет наибольшую частоту. Далее по формуле рассчитываем моду:
| Медиана – это значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Основное свойство медианы: сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Определение медианы: 1) по несгруппированным данным. Для начала выстоим ранжированный ряд: 4,2; 4,3; 4,3; 4,3; 4,4; 4,4; 4,5; 4,6; 4,6. Центральной в ряду является цена 4,4 тыс. руб. Причем, если ранжированный ряд имеет четное число единиц, то медиана определяется как средняя из двух центральных значений. 2) по сгруппированным данным: - по дискретным рядам: Сначала находим номер медианной единицы ряда по формуле:
В нашем случае Nme = (190 - 1) : 2 = 95,5. Это означает, что точная середина находится между 95-ой и 96-ой организацией. Чтобы определить группу, к которой относятся организации с этими порядковыми номерами. Рассчитаем накопленные частоты 12+48=40; 12+48+56 =116. А значит организации с порядковыми номерами 95 и 96 относятся к группе организаций продающих товар А по цене 54 руб. – это цена и есть медиана. - по интервальным рядам медиана определяется по формуле:
где xMe — нижняя граница медианного интервала; iMe — ширина медианного интервала; ∑f/2 — количество всех значений, деленное на 2 (два); S(Me-1)— накопленная частота интервала, предшествующая медианному; fMe — частота медианного интервала.
Пример:Для определения медианного интервала рассчитываем накопленную частоту каждого последующего интервала до тех пор пока она не превысит ½ суммы накопленных частот (в нашем случае 73,35 = 146,7 : 2): 22,1+27,8=49,9; 22,1+27,8+25,2 = 75,1. А значит, интервал 600-800 является медианным.
Рассчитываем медиану по формуле:
|
Дата добавления: 2017-04-20; просмотров: 1148;

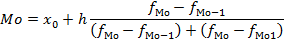
 Распределение населения РФ по уровню
Распределение населения РФ по уровню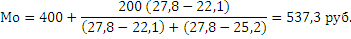
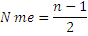 где n – объем совокупности
где n – объем совокупности