Аналитические и статистические методы

Эти группы методов получили наибольшее распространение в практике проектирования и управления. Правда, для представления промежуточных и окончательных результатов моделирования широко используются графические представления (графики, диаграммы и т.п.). Однако последние являются вспомогательными; основу же модели, доказательства её адекватности составляют те или иные направления аналитических и статистических представлений. Поэтому кратко охарактеризуем их особенности, достоинства и недостатки с точки зрения возможности использования при моделировании систем.

Аналитическими в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек (безразмерных в строгих математических доказательствах), совершающих какие-либо перемещения в абстрактном пространстве или взаимодействующих между собой.

Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.).

Аналитические представления имеют многовековую историю развития, и для них характерно не только стремление к строгости терминологии, но и к закреплению за некоторыми специальными величинами определённых букв (например, удвоенное отношение площади круга к площади вписанного в него квадрата π=3,1415; основание натурального логарифма – е=2,718 и т.д.).

На базе аналитических представлений возникли и развиваются математические теории различной сложности – от аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т.п.) до таких новых разделов современной математики, как математическое программирование (линейное, нелинейное, динамическое и т.п.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т.п.).

Эти теоретические направления стали основой многих прикладных, в том числе теории автоматического управления, теории оптимальных решений и т.д.

При моделировании систем применяется широкий спектр символических представлений, использующих «язык» классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математическими моделями.

Большинство из направлений математики не содержат средств постановки задачи и доказательства адекватности модели. Последняя доказывается экспериментом, который по мере усложнения проблем становится также всё более сложным, дорогостоящим, не всегда бесспорен и реализуем.

В то же время в состав этого класса методов входит относительно новое направление математики – математическое программирование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности моделей.

Статистические представления сформировались как самостоятельное научное направление в середине прошлого века (хотя возникли значительно раньше). Основу их составляет отображение явлений и процессов с помощью случайных (стохастических) событий и их поведений, которые описываются соответствующими вероятностными (статистическими) характеристиками и статистическими закономерностями.

Статистические отображения системы в общем случае (по аналогии с аналитическими) можно представить как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (или её учитываемые в модели свойства) оператор Ф[S_x]. «Размытую» точку следует понимать как некоторую область, характеризующую движение системы (её поведение); при этом границы области заданы с некоторой вероятностью p («размыты») и движение точки описывается некоторой случайной функцией.

Закрепляя все параметры этой области, кроме одного, можно получить срез по линии а – b, смысл которого – воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру. Аналогично можно получить двумерную, трёхмерную и т.д. картины статистического распределения.

Статистические закономерности можно представить в виде дискретных случайных величин и их вероятностей, или в виде непрерывных зависимостей распределения событий, процессов.

Для дискретных событий соотношение между возможными значениями случайной величины x_i и их вероятностями p_i, называют законом распределения и либо записывают в виде ряда (табл. 2.1), либо представляют в виде зависимостей F(x) (рис. 2.2, а) или p(х) (рис. 2.2, в).

Для непрерывных случайных величин (процессов) закон распределения представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения – рис. 2.2, б), либо в виде плотности вероятностей (дифференциальный закон распределения – рис. 2.2, г). В этом случае

р(х) = dF(x) / dx,

где р(х) – вероятность попадания случайных событий в интервал от х до х + dх.

Закон распределения является удобной формой статистического отображения системы. Однако получение закона (даже одномерного) или определение изменений этого закона при прохождении через какие-либо устройства или среды представляет собой трудную, часто невыполнимую задачу. Поэтому в ряде случаев пользуются не распределением, а его характеристиками – начальными и центральными моментами.

Наибольшее применение получили:

первый начальный момент – математическое ожидание или среднее значение случайной величины:

– для дискретных величин

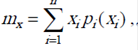
– для непрерывных величин

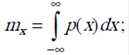
второй центральный момент – дисперсия случайной величины:

– для дискретных величин

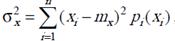
– для непрерывных величин

.

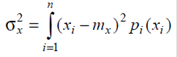На практике иногда используется не дисперсия, а среднее квадратическое отклонение.