Методы моделирования систем

Постановка любой задачи заключается в том, чтобы перевести её словесное, вербальное описание в формальное. В случае относительно простых задач такой переход осуществляется в сознании человека, который не всегда даже может объяснить, как он это сделал. Если полученная формальная модель (математическая зависимость между величинами в виде формулы, уравнения, системы уравнений) опирается на фундаментальный закон или подтверждается экспериментом, то этим доказывается её адекватность отображаемой ситуации, и модель рекомендуется для решения задач соответствующего класса.

По мере усложнения задач получение модели и доказательство её адекватности усложняется. Вначале эксперимент становится дорогим и опасным (например, при создании сложных технических комплексов, при реализации космических программ и т.д.), а применительно к экономическим объектам эксперимент становится практическим нереализуемым, задача переходит в класс проблем принятия решений, и постановка задачи, формирование модели, т.е. перевод вербального описания в формальное, становится важной составной частью процесса принятия решения. Причём эту составную часть не всегда можно выделить как отдельный этап, завершив который, можно обращаться с полученной формальной моделью так же, как с обычным математическим описанием, строгим и абсолютно справедливым. Большинство реальных ситуаций проектирования сложных технических комплексов и управления экономикой необходимо отображать классом самоорганизующихся систем, модели которых должны постоянно корректироваться и развиваться.

При этом возможно изменение не только модели, но и метода моделирования, что часто является средством развития представления ЛПР о моделируемой ситуации. Иными словами, перевод вербального описания в формальное, осмысление, интерпретация модели и получаемых результатов становятся неотъемлемой частью практически каждого этапа моделирования сложной развивающейся системы.

Часто для того чтобы точнее охарактеризовать такой подход к моделированию процессов принятия решений, говорят о создании «механизма» моделирования, «механизма» принятия решений (например, «хозяйственный механизм», «механизм проектирования и развития предприятия» и т.п.).

Возникающие вопросы – как формировать такие развивающиеся модели или «механизмы»? как доказывать адекватность моделей? – и являются основным предметом системного анализа.

Для решения проблемы перевода вербального описания в формальное в различных областях деятельности стали развиваться специальные приёмы и методы. Так, возникли методы типа «мозговой атаки», «сценариев», экспертных оценок, «дерева целей» и т.п.

В свою очередь, развитие математики шло по пути расширения средств постановки и решения трудноформализуемых задач. Наряду с детерминированными, аналитическими методами классической математики возникла теория вероятностей и математическая статистика (как средство доказательства адекватности модели на основе представительной выборки и понятия вероятности правомерности использования модели и результатов моделирования). Для задач с большей степенью неопределённости инженеры стали привлекать теорию множеств, математическую логику, математическую лингвистику, теорию графов, что во многом стимулировало развитие этих направлений. Иными словами, математика стала постепенно накапливать средства работы с неопределённостью, со смыслом, который классическая математика исключала из объектов своего рассмотрения.

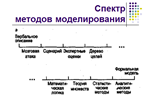Таким образом, между неформальным, образным мышлением человека и формальными моделями классической математики сложился как бы «спектр» методов, которые помогают получать и уточнять (формализовать) вербальное описание проблемной ситуации, с одной стороны, и интерпретировать формальные модели, связывать их с реальной действительностью, с другой. Этот спектр условно представлен на рис. 2.1, а.

Развитие методов моделирования, разумеется, шло не так последовательно, как показано на рис. 2.1, а. Методы возникали и развивались параллельно. Существуют различные модификации сходных методов. Их по-разному объединяли в группы, т.е. исследователи предлагали разные классификации (в основном – для формальных методов, что более подробно будет рассмотрено в следующем параграфе). Постоянно возникают новые методы моделирования как бы на «пересечении» уже сложившихся групп. Однако основную идею – существование «спектра» методов между вербальным и формальным представлением проблемной ситуации – этот рисунок иллюстрирует.

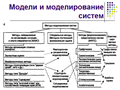Первоначально исследователи, развивающие теорию систем, предлагали классификации систем и старались поставить им в соответствие определённые методы моделирования, позволяющие наилучшим образом отразить особенности того или иного класса. Такой подход к выбору методов моделирования подобен подходу прикладной математики. Однако в отличие от последней, в основу которой положены классы прикладных задач, системный анализ может один и тот же объект или одну и ту же проблемную ситуацию (в зависимости от степени неопределённости и по мере познания) отображать разными классами систем и соответственно различными моделями, как бы организовывая таким образом процесс постепенной формализации задачи, т.е. «выращивание» её формальной модели. Подход помогает понять, что неверно выбранный метод моделирования может привести к неверным результатам, к невозможности доказательства адекватности модели, к увеличению числа итераций и затягиванию решения проблемы.