Теоретико-множественные представления

Теоретико-множественные представления базируются на понятиях множество, элементы множества, отношения на множествах.

Понятие множество относится к числу интуитивно постигаемых понятий, которым трудно дать определение. Это понятие содержательно эквивалентно понятиям «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «класс» и другим обобщающим понятиям. Один из основоположников теории множеств Георг Кантор определял множество как «многое, мыслимое нами как единое».

Множества могут задаваться следующими способами:

1) списком, перечислением (интенсиональным путём);

например, {ai}, где i = 1, …, n, или <a1, a2, …, ai, …, an>,

где 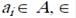– знак вхождения элементов в множество;

2) путём указания некоторого характеристического свойства А (экстенсионально). Например, «множество натуральных чисел», «множество рабочих данного завода», «множество планет солнечной системы», «множество А» и т.д.

В основе теоретико-множественных преобразований лежит принцип перехода от одного способа задания множества к другому:

A = <a1, a2, …, ai, …, an>,

или

<a1, a2, …, ai, …, an> →A.

Переход от интенсионального способа задания множества к экстенсиональному называют принципом свёртывания.

В множестве могут быть выделены подмножества. Вхождение элементов в любое множество или подмножество описывается знаком принадлежит – 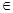, а вхождение подмножества в множество записывается В 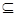А. Это означает, что все элементы подмножества В являются одновременно элементами множества А (рис. 2.3):

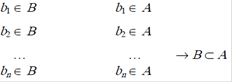
Важным понятием является понятие пустое множество – множество, в котором в данный момент нет ни одного элемента: .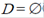

При использовании теоретико-множественных представлений в соответствии с концепцией Кантора можно вводить любые отношения. При уточнении этих отношений применительно к множествам удобно пользоваться наглядными диаграммами Эйлера- Венна, примеры которых для операции объединения, пересечения, дополнения (отрицания, обозначаемого знаком «–» над именем множества, либо знаком перед именем множества или его элемента) приведены в табл. 2.2.