Теория функционала плотности

Как показано выше, учет корреляционной энергии молекулы в вычислительном отношении является весьма трудной задачей. Относительно простой подход представляет собой т.н. теория функционала плотности, которая позволяет значительно улучшить точность расчета энергии сложных систем, требуя при этом значительно меньше времени и ресурсов, чем ab initio методы MPn, CCSD, QCISD, CI и т.д. Основное отличие ТФП от методов ab intio состоит в том, что система описывается не волновой функцией, а электронной плотностью ρ(r), определяемой как:

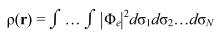
Здесь Φ_e - многоэлектронная ВФ системы, σ_i - cовокупность спиновых и пространственных координат электронов, N - число электронов. Таким образом ρ(r) есть функция только трех пространственных координат rточки, в которой ρ(r) дает вероятность обнаружения какого-либо из электронов молекулы.

Практическое применение ТФП - это две теоремы, доказанные Хоэнбергом и Коном в 1964 г. и обобщенные затем несколькими авторами. Первая теорема (теорема Хоэнберга-Кона) утверждает, что любое свойство основного состояния данной системы описывается только электронной плотностью ρ(r) (и не требует знания волновой функции). Важно подчеркнуть, что эта теорема доказана только для основного состояния молекулы и, строго говоря, ТФП не является точной теорией для возбужденных состояний.

Вторая теорема устанавливает вариационный принцип в ТФП: если E₀ – точная энергия основного состояния, то для любой другой электронной плотности ρ, которая может быть и приближением к истинной электронной плотности основного состояния, выполняется соотношение E[ρ] ≥ E₀. Это утверждение, как и в методах, основанных на фолоновой функции, дает метод нахождения E₀ и соответствующей плотности.

Если любое свойство основного состотяния молекулы может быть выражено через ρ, то электронная энергия в ТФП есть:

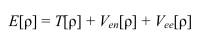
Здесь T[ρ] - кинетическая энергия, V_en[ρ] - потенциальная энергия электронно-ядерных взаимодействий, V_ee[ρ] - энергия межэлектронных взаимодействий:

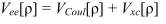
Здесь V_Coul[ρ] - энергия кулоновского взаимодействия электронов, а V_xc[ρ] -т.н. обменно-корреляционная энергия. Функционалы T[ρ], V_en[ρ] и V_Coul[ρ] могут быть найдены точно, аналогично методу Хартри-Фока. Наиболее простой способ этого представляет собой т.н. метод Кона-Шэма. В этом методе ρ представляется как сумма вкладов отдельных электронов, описывающихся некими вспомогательными самосогласованными орбиталями (орбиталями Кона-Шэма):

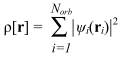
Для обменно-корреляционного потенциала V_xc[ρ] однако, точное представление не известно и требуется введение дополнительных приближений: приближение локальной плотности, приближение локальной спиновой плотности или обобщенное градиентное приближение.

Сама обменно-корреляционная энергия, как уже было сказано, точно не известна и существуют большое число моделей для ее описания. Различные варианты формулы (6.8) и (6.9) приводят, таким образом, к различным вариантам ТФП. Говорят, что ТФП используется с различными функционалами. Наиболее известные и широко используемые среди них функционалы Бекке-Пердью (BP), Пердью-Ванга (PW91), Бекке-Ли-Янга-Парра (BLYP) и Пердью-Бёрке-Эрнцерхофа (PBE).

Отметим, что во многих случаях нелокальная обменная энергия описывается локальным обменным функционалом. Такое упрощение не может не привести к погрешностям. Для того, чтобы бороться с ними, было предложено включать в V_xc точный Хартри-Фоковский обменный оператор, рассматривая его как одну из моделей для описания обменной энергии. Оказалось, что такой способ дает значительный выигрыш в точности, особенно, если комбинировать его с некоторыми другими обменными функционалами. В результате появилось семейство т.н. параметрических функционалов, среди которых наиболее известен B3LYP - функционал, включающий три компоненты обменного функционала (точный Хартри-Фоковский обменный оператор, функционал Бекке и функционал Слейтера, а корреляционная часть представляет собой комбинацию функционалов Ли-Янга-Парра (LYP) и Воско-Вилка-Нусара (VWN)). Особенностью этого подхода является то, что три обменные компоненты берутся с весовыми коэффициентами, подобранными на основе сравнения с экспериментальными данными.

В настоящее время появилось большое число новых функционалов, точность которых приближается к точности B3LYP, а в ряде случаев и превосходит его. Следует упомянуть функционал OLYP (комбинация обменного функционала OPTX и корреляционного LYP), функционал Хампрехта-Коэна-Тозера-Хэнди (HCTH) и уже упоминавшийся функционал PBE.

Как только обменно-корреляционный потенциал задан, решение методом ТФП проводится путем решения т.н. уравнений Кона-Шэма:

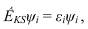
Как только система (6.10) задана, процедура ее решения полностью аналогична процедуре самосогласования метода Хартири-Фока. Тот факт, что в ТФП не требуется расчет обменных интегралов и не нужны специальные методы для уточнения корреляционной энергии приводит к тому, что по вычислительной эффективности ТФП становится одним из наиболее предпочтительных методов. Использование ТФП позволяет рассчитывать большие молекулярные системы (включающих десятки и сотни, а иногда и тысячи атомов) с затратами, сравнимыми с методом Хартри-Фока, а по точности значительно превосходящей его.

Точность ТФП в варианте B3LYP при расчетах структуры молекул, энергии реакций, колебательных частот, электронных моментов сравнима с точностью метода MP2. При этом время, требуемое для расчета, почти на порядок меньше. В ряде случаев (например, при расчете колебательных частот), точность функционала B3LYP превосходит все известные неэмпирические методы.

Один из недостатков ТФП - это то, что метод ориентирован только на расчет свойств систем с невырожденными оболочками и основного состояния молекул. Однако, существуют расширения этого метода на системы с вырождением (т.н. метод ROKS, restricted open-shell Kohn-Sham), который является аналогом метода ROHF. Для расчета возбужденных состояний создан специальный вариант ТФП, т.н. времязависимая теория возмущений (TD-DFT, time-dependent DFT), который в настоящее время рассматривается как один из наиболее перспективных методов оценки энергий возбуждения.

Важный недостаток ТФП при расчетах основного состояния состоит в том, что эта теория учитывает энергию корреляции только для небольшого диапазона возбуждений. Этого достаточно для описания свойств свободных молекул. Однако при попытке описания слабовзаимодействующих комплексов, для которых основной вклад в энергию связи дают дисперсионное взаимодействие, ТФП дает большую ошибку.