АРИФМЕТИКА. Теория делимости 1 страница
В этой главе основным множеством будет кольцо целых рациональных чисел. Так как традиционная арифметика занимается, как правило, свойствами обычных целых чисел. Начнем с известных результатов.
Определение 13.1. Пусть 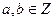 и
и 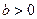 . Тогда говорим, что
. Тогда говорим, что  делится на
делится на 
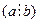 , или
, или  делит
делит 
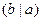 , если существует такое
, если существует такое 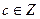 , что выполняется равенство
, что выполняется равенство
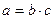 .
.
Число  называют делимым, а число
называют делимым, а число  – делителем (рассматриваем положительные делители).
– делителем (рассматриваем положительные делители).
Рассмотрим некоторые простейшие свойства делимости.
1.  Если
Если 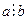 и
и 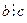 , то
, то 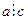 . Таким образом, бинарное отношение делимости обладает свойством транзитивности.
. Таким образом, бинарное отношение делимости обладает свойством транзитивности.
2.  Если
Если 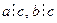 , то
, то 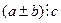 .
.
3.  Если
Если 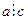 , то для любого
, то для любого 
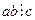 .
.
4.  Если
Если 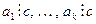 , то для любых
, то для любых 
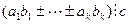 .
.
5.  Любое число делится на 1.
Любое число делится на 1.
Проверку свойств оставляем студентам.
Теорема 13.1 (о делении с остатком).
Пусть 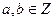 и
и 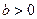 . Тогда существуют однозначно определенные целые числа
. Тогда существуют однозначно определенные целые числа 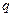 и
и 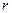 такие, что выполняется равенство
такие, что выполняется равенство
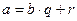 , (13.1)
, (13.1)
где  . Число
. Число 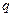 называется неполным частным, а число
называется неполным частным, а число 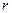 – остатком от деления.
– остатком от деления.
Доказательство. Существование. Если  , то выбираем ближайшее к
, то выбираем ближайшее к  кратное числу
кратное числу  и не превосходящее
и не превосходящее  , т.е.,
, т.е., 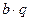 , а тогда
, а тогда 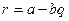 . Если
. Если 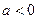 , то снова выбираем ближайшее к
, то снова выбираем ближайшее к  кратное числу
кратное числу  и не превосходящее
и не превосходящее  , но уже с отрицательным
, но уже с отрицательным 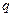 . И тогда опять
. И тогда опять 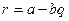 . Случай
. Случай 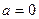 тривиален.
тривиален.
Единственность. Если предположить, что существуют два различных представления вида (13.1), например, 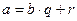 и
и 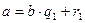 такие, что
такие, что  и
и 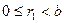 , то, вычитая из первого второе, получаем
, то, вычитая из первого второе, получаем
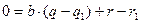 ,
,
т.е.,
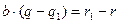 .
.
Так как 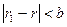 , то
, то  не может делить такое число, если оно не равно нулю. Получаем противоречие. Значит,
не может делить такое число, если оно не равно нулю. Получаем противоречие. Значит, 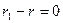 , а тогда
, а тогда  , но и
, но и 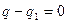 , т.е.
, т.е. 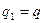 . Теорема доказана.
. Теорема доказана.
Определение 13.2. Если  и
и 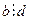 , то число
, то число 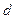 называется общим делителем чисел
называется общим делителем чисел  и
и  , а наибольшее из них называется наибольшим общим делителем (НОД) и обозначается
, а наибольшее из них называется наибольшим общим делителем (НОД) и обозначается 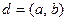 .
.
Существование НОД двух целых чисел не вызывает сомнений. Остается указать способ нахождения такого числа. Но предварительно отметим следующие результаты.
Лемма 13.1. Если 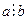 , то совокупность общих делителей
, то совокупность общих делителей  и
и  совпадает с совокупностью делителей числа
совпадает с совокупностью делителей числа  . Значит, в частности,
. Значит, в частности, 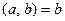 .
.
Лемма 13.2. Если три целых числа 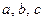 связанны соотношением
связанны соотношением
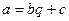 ,
,
то совокупность общих делителей  и
и  совпадает с совокупностью общих делителей
совпадает с совокупностью общих делителей  и
и 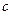 . В частности,
. В частности, 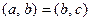 .
.
Алгоритм Евклида.
Пусть требуется найти НОД двух натуральных чисел  и
и  . Для определенности считаем, что
. Для определенности считаем, что 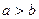 . Тогда применим следующую процедуру деления с остатком.
. Тогда применим следующую процедуру деления с остатком.
 ,
, 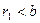 ;
;
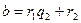 ,
,  ;
;
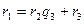 ,
, 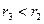 ;
;
. . . . . . . . . . .
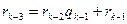 ,
,  ;
;
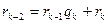 ,
, 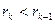 ;
;
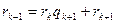 ,
, 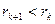 ;
;
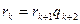 ;
;
Легко понять, что при данном процессе остатки от деления образуют строго убывающую последовательность целых неотрицательных чисел, что в итоге обязательно приводит к остатку, равному 0. Покажем, что последний отличный от нуля остаток и будет наибольшим общим делителем чисел  и
и  . В данном случае это будет
. В данном случае это будет 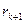 . Действительно, применим лемму 13.2. Имеем
. Действительно, применим лемму 13.2. Имеем
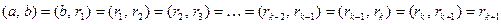 .
.
Последнее равенство получается по лемме 13.1.
Кроме того, можно заметить, что НОД чисел  и
и  делится на любой их общий делитель в соответствии с той же леммой 13.2.
делится на любой их общий делитель в соответствии с той же леммой 13.2.
Пример 13.1. Пусть требуется найти 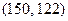 . Применим алгоритм Евклида. Имеем
. Применим алгоритм Евклида. Имеем

Последний отличный от нуля остаток равен 2. Значит, 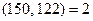 .
.
Теорема 13.2 (линейное представление НОД двух чисел).
Пусть 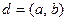 . Тогда существуют такие целые
. Тогда существуют такие целые 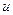 и
и 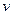 , что
, что 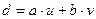 .
.
Доказательство. Воспользуемся равенствами из алгоритма Евклида. Они позволяют записать, что

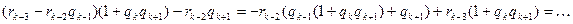 .
.
Заменяя последовательно остатки на предшествующие остатки и неполные частные, поднимаясь по лестнице равенств, в итоге выразим число 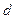 указанным в формулировке образом.
указанным в формулировке образом.
Отметим свойства НОД двух чисел.
1. 
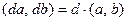
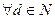 .
.
2. 
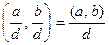 .
.
3. 
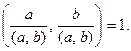
Доказательства оставим студентам и дадим еще одно определение.
Определение 13.3. Числа  и
и  называются взаимно простыми, если их наибольший общий делитель равен 1.
называются взаимно простыми, если их наибольший общий делитель равен 1.
Опишем некоторые свойства взаимно простых чисел.
1.  Если
Если 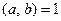 и
и 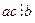 , то
, то 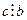 .
.
2.  Если
Если 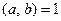 и
и 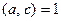 , то
, то 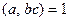 .
.
3.  Если
Если 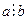 и
и 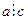 , то при
, то при 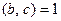
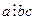 .
.
4.  Если
Если 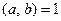 , то
, то 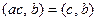 .
.
5.  Если
Если 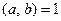 , то существуют такие целые
, то существуют такие целые 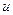 и
и 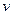 , что
, что 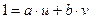 . Это свойство есть прямое следствие теоремы 13.2.
. Это свойство есть прямое следствие теоремы 13.2.
Доказательство 1  . Воспользуемся свойством 5
. Воспользуемся свойством 5  . Имеем
. Имеем
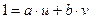 .
.
Умножим обе части равенства на с, получим
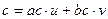 .
.
Тогда, так как  делит первое и второе слагаемое, по второму свойству делимости на
делит первое и второе слагаемое, по второму свойству делимости на  делится и сумма, т.е., с.
делится и сумма, т.е., с.
Доказательство остальных свойств оставляем студентам.
Определение 13.4. Пусть заданы два натуральных числа  и
и  , тогда натуральное число, делящееся на эти числа, называется их общим кратным, наименьшее из которых называется наименьшим общим кратным (НОК) и обозначается
, тогда натуральное число, делящееся на эти числа, называется их общим кратным, наименьшее из которых называется наименьшим общим кратным (НОК) и обозначается 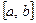 .
.
Лемма 13.3. Пусть 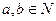 , тогда
, тогда 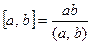 .
.
Доказательство. Пусть 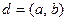 , тогда
, тогда 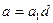 ,
, 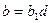 . При этом
. При этом 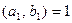 по свойству 3
по свойству 3  НОД. Поэтому, если М – какое-либо кратное
НОД. Поэтому, если М – какое-либо кратное  и
и  , то М кратно а и, значит,
, то М кратно а и, значит, 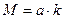 , для некоторого
, для некоторого 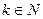 . Но М кратно и
. Но М кратно и  , так что
, так что
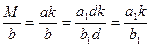 .
.
Так как полученное число должно быть целым, то по первому свойству взаимно простых чисел 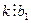 , т.е.,
, т.е., 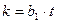 ,
, 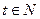 . Следовательно, отсюда получаем, что
. Следовательно, отсюда получаем, что
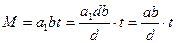 .
.
Отсюда ясно, что при любом 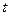 число М будет общим кратным чисел
число М будет общим кратным чисел  и
и  , а наименьшим общим кратным при
, а наименьшим общим кратным при 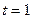 .
.
Следствие 1. Произвольное общее кратное чисел  и
и  – М удовлетворяет соотношению
– М удовлетворяет соотношению 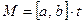 ,
, 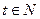 .
.
Следствие 2. Если 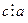 и
и  , то
, то 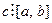 .
.
Простые числа
Начнем с определения простого числа.
Определение 13.5. Натуральное число 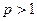 называется простым, если имеет только тривиальные делители, т.е., делятся только на 1 и самого себя.
называется простым, если имеет только тривиальные делители, т.е., делятся только на 1 и самого себя.
Определение 13.6. Натуральные числа, не являющиеся простыми, называются составными.
Рассмотрим несколько простых результатов, касающихся простых чисел.
Лемма 13.4. Наименьший не равный 1 делитель целого, большего 1, – число простое. Доказательство. Пусть этот делитель 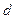 числа
числа  не является простым, т.е., составное число. Тогда существует представление
не является простым, т.е., составное число. Тогда существует представление 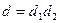 , где
, где 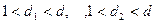 . А это противоречит тому, что
. А это противоречит тому, что 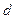 наименьший делитель, ибо по первому свойству делимости, например,
наименьший делитель, ибо по первому свойству делимости, например, 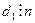 .
.
Лемма 13.5. Наименьший отличный от 1 делитель составного числа  не превосходит
не превосходит 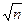 .
.
Доказательство. Пусть 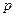 будет наименьшим делителем числа
будет наименьшим делителем числа  по условию леммы. Тогда
по условию леммы. Тогда  . При этом
. При этом 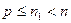 . Следовательно,
. Следовательно, 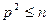 , откуда и получается требуемое неравенство.
, откуда и получается требуемое неравенство.
Теорема 13.3 (Евклида).
Простых чисел бесконечно много.
Доказательство. Докажем теорему от противного. Пусть 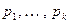 – все существующие простые числа. Рассмотрим число
– все существующие простые числа. Рассмотрим число 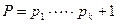 . Это число по предположению должно быть составным. И тогда у него есть нетривиальные делители, среди которых должен присутствовать наименьший, т.е., некоторое простое число из имеющихся, например,
. Это число по предположению должно быть составным. И тогда у него есть нетривиальные делители, среди которых должен присутствовать наименьший, т.е., некоторое простое число из имеющихся, например, 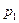 . Но число
. Но число  не делится на
не делится на 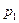 , ибо по свойствам делимости тогда и единица должна была бы делится на
, ибо по свойствам делимости тогда и единица должна была бы делится на 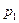 , а
, а 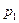 , будучи простым, больше единицы. Противоречие доказывает теорему.
, будучи простым, больше единицы. Противоречие доказывает теорему.
Это, наверное, самое простое доказательство факта бесконечности простых, хотя имеются многие другие и весьма сложные. Еще в древности был найден способ выписывания последовательности всех простых, не превосходящих некоторой величины. Метод этот называется решетом Эратосфена и заключается в следующем. Задается число-граница 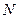 , до которой следует выписать все простые числа без пропусков. Составляется ряд натуральных чисел от 2 до
, до которой следует выписать все простые числа без пропусков. Составляется ряд натуральных чисел от 2 до 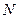 и затем начинают процедуру «просеивания». Именно, из последовательности вычеркиваются все числа, кратные 2. Первым не вычеркнутым числом оказывается 3. Поэтому оно простое. Теперь вычеркиваются все числа, кратные 3. И видим, первым не вычеркнутым оказывается число 5, так как 4 вычеркнуто в предыдущий раз. Тогда 5 – простое число. Затем вычеркиваются числа, кратные 5 и т.д. Возникает вопрос: когда процесс можно завершить? Ответ дает лемма 13.5, т.е., требуется перебрать простые
и затем начинают процедуру «просеивания». Именно, из последовательности вычеркиваются все числа, кратные 2. Первым не вычеркнутым числом оказывается 3. Поэтому оно простое. Теперь вычеркиваются все числа, кратные 3. И видим, первым не вычеркнутым оказывается число 5, так как 4 вычеркнуто в предыдущий раз. Тогда 5 – простое число. Затем вычеркиваются числа, кратные 5 и т.д. Возникает вопрос: когда процесс можно завершить? Ответ дает лемма 13.5, т.е., требуется перебрать простые 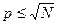 и через них «просеять» указанный ряд. Учитывая, что
и через них «просеять» указанный ряд. Учитывая, что 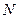 гораздо больше
гораздо больше 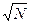 , получаем, что, используя сравнительно малый отрезок простых, можно получить большой массив простых чисел. С точки зрения эффективности эта процедура достаточно медленная и требующая много памяти. Но для небольших
, получаем, что, используя сравнительно малый отрезок простых, можно получить большой массив простых чисел. С точки зрения эффективности эта процедура достаточно медленная и требующая много памяти. Но для небольших 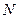 вполне приемлемая. Простым числам посвящено множество исследований, но здесь ограничимся необходимым минимумом.
вполне приемлемая. Простым числам посвящено множество исследований, но здесь ограничимся необходимым минимумом.
Лемма 13.6. Всякое целое число  или взаимно просто с простым
или взаимно просто с простым 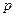 , или делится на него.
, или делится на него.
Доказательство. Пусть 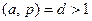 . Тогда
. Тогда 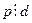 и, значит,
и, значит, 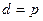 .
.
Лемма 13.7. Если произведение нескольких целых чисел делится на простое число 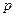 , то, по крайней мере, один из сомножителей делится на
, то, по крайней мере, один из сомножителей делится на 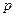 .
.
Доказательство. Достаточно доказать для двух сомножителей. Пусть 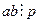 . Если
. Если 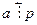 , то
, то 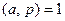 , тогда по первому свойству взаимно простых чисел
, тогда по первому свойству взаимно простых чисел  .
.
Теорема 13.4 (основная теорема арифметики).
Каждое натуральное число, большее 1, разлагается в произведение простых сомножителей. Такое разложение единственно с точностью до порядка следования этих сомножителей.
Доказательство. Существование. Пусть число 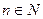 и
и 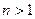 . Тогда если
. Тогда если  – простое, то разложение получено, а если оно составное, то его можно представить в виде
– простое, то разложение получено, а если оно составное, то его можно представить в виде  , где
, где 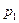 есть наименьший делитель отличный от 1. Отсюда заключаем, что
есть наименьший делитель отличный от 1. Отсюда заключаем, что 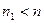 . И вновь, если
. И вновь, если 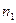 – число простое, то разложение получено. Иначе,
– число простое, то разложение получено. Иначе,  , где уже
, где уже 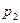 суть наименьший нетривиальный делитель
суть наименьший нетривиальный делитель 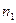 . Тогда имеем:
. Тогда имеем: 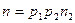 , и
, и 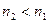 . Продолжая этот процесс, видим, что последовательность нумерованных
. Продолжая этот процесс, видим, что последовательность нумерованных 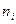 ,
, 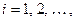 строго убывает. Поэтому в силу ограниченности натурального ряда снизу этот процесс обязательно завершится, выделив в последнем случае простое число. Тогда получим представление
строго убывает. Поэтому в силу ограниченности натурального ряда снизу этот процесс обязательно завершится, выделив в последнем случае простое число. Тогда получим представление
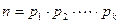 . (13.2)
. (13.2)
Единственность. Пусть существует еще одно представление  в виде произведения простых, а именно:
в виде произведения простых, а именно: 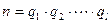 . Приравняем полученные разложения.
. Приравняем полученные разложения.
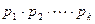
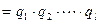 .
.
В соответствии с леммой 13.7 число 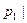
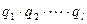 и, значит, должно делить какой-то из сомножителей
и, значит, должно делить какой-то из сомножителей 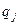 ,
, 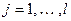 . Пусть это будет
. Пусть это будет 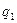 . Но так как
. Но так как 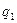 само простое, то это возможно лишь при
само простое, то это возможно лишь при  . Сократив равенство на общий множитель
. Сократив равенство на общий множитель 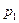 , получим соотношение
, получим соотношение
Дата добавления: 2019-07-26; просмотров: 818;
