АРИФМЕТИКА. Теория делимости 5 страница
Доказательство. Рассмотрим ряд чисел 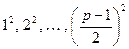 . Все они, очевидно, являются квадратичными вычетами по модулю
. Все они, очевидно, являются квадратичными вычетами по модулю  . Но квадратичными вычетами будут те и только те числа, которые сравнимы с квадратами ПрСВ. Остается показать, что указанные квадраты представляют различные классы по модулю
. Но квадратичными вычетами будут те и только те числа, которые сравнимы с квадратами ПрСВ. Остается показать, что указанные квадраты представляют различные классы по модулю  . Если напротив найдутся такие
. Если напротив найдутся такие 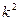 и
и  , где
, где 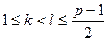 , такие, что
, такие, что 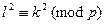 , то
, то 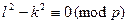 и
и 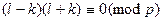 . Значит,
. Значит, 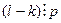 или
или 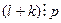 , что невозможно. Лемма доказана.
, что невозможно. Лемма доказана.
Определение 13.19. Пусть  – простое нечетное. Символом Лежандра
– простое нечетное. Символом Лежандра 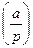 (читается «
(читается « 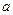 по
по  ») называется арифметическая функция, определяемая равенством:
») называется арифметическая функция, определяемая равенством:
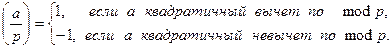
Это определение иногда для удобства дополняют значением 0 для 
Вычисление символов Лежандра возможно при помощи следующей теоремы.
Теорема 13.15 (критерий Эйлера).
Если 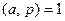 , то
, то
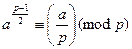 .
.
Доказательство. В соответствии с малой теоремой Ферма (см. следствие 1 из т.13.8) имеем 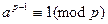 . Это приводит к сравнению
. Это приводит к сравнению
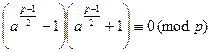 .
.
Содержимое двух полученных скобок не может одновременно делиться на  , ибо тогда на
, ибо тогда на  делилась бы их разность, а она равна 2, что невозможно. Тогда имеет место одно из сравнений
делилась бы их разность, а она равна 2, что невозможно. Тогда имеет место одно из сравнений
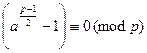
или
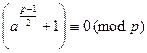 .
.
Всякий квадратичный вычет 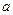 должен удовлетворять сравнению
должен удовлетворять сравнению 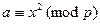 для некоторого х. А значит и сравнению, полученному из данного возведением обеих частей в степень
для некоторого х. А значит и сравнению, полученному из данного возведением обеих частей в степень 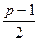 , т.е.,
, т.е.,
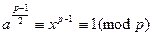 .
.
Следовательно, выполняется первое сравнение. Учитывая, что сравнение
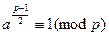
не может удовлетворяться большим количеством решений чем 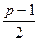 по теореме 13.13,
по теореме 13.13,
то остальные вычеты ПрСВ удовлетворяют второму сравнению, являясь квадратичными невычетами по модулю  .
.
Пример 13.23. Пусть 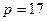 , а
, а 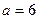 , тогда так как
, тогда так как 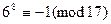 , то
, то 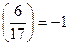 и значит 6 – квадратичный невычет по модулю 17.
и значит 6 – квадратичный невычет по модулю 17.
Пример 13.24. Пусть  , а
, а 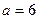 , тогда так как
, тогда так как 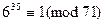 , то
, то 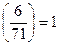 и значит 6 – квадратичный вычет по модулю 71.
и значит 6 – квадратичный вычет по модулю 71.
Рассмотрим свойства символа Лежандра.
1. 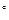
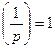 ;
;
2. 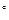
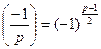 ;
;
3. 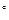
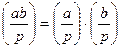 ;
;
4. 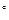
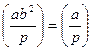 ;
;
5. 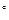
 ;
;
6. 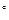
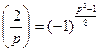 .
.
Доказательства первых пяти весьма просты. Действительно, первое свойство очевидно. Второе легко следует из теоремы 13.15 с 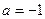 . Кстати, можно в этом случае вычислять символ и иначе: если
. Кстати, можно в этом случае вычислять символ и иначе: если 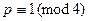 , то значение символа равно 1, а если
, то значение символа равно 1, а если  , то значение равно -1. После третьего свойства убеждаемся, что символ – вполне мультипликативная функция. А доказательство можно провести так:
, то значение равно -1. После третьего свойства убеждаемся, что символ – вполне мультипликативная функция. А доказательство можно провести так:
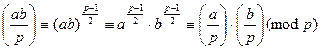 .
.
Легко видеть, что отношение сравнимости здесь превращается в отношение равенства. Четвертое свойство является прямым следствием третьего. Пятое свойство вновь следует из теоремы 13.15. Наконец, свойство 6 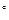 придется доказывать аккуратно. Введем для простоты обозначение
придется доказывать аккуратно. Введем для простоты обозначение 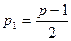 и рассмотрим ряд сравнений (считаем, что
и рассмотрим ряд сравнений (считаем, что 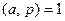 ):
):

где 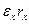 – абсолютно наименьший вычет
– абсолютно наименьший вычет 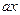 , при этом
, при этом 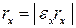 ,
,  . По лемме 13.25 числа
. По лемме 13.25 числа  , где
, где 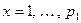 , пробегают приведенную систему вычетов по модулю
, пробегают приведенную систему вычетов по модулю  , а
, а 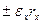 ,
, 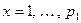 , их абсолютно наименьшие вычеты. Из последних положительные должны совпадать с числами
, их абсолютно наименьшие вычеты. Из последних положительные должны совпадать с числами  . Перемножим теперь выписанные выше сравнения и сократим обе части полученного сравнения на величину
. Перемножим теперь выписанные выше сравнения и сократим обе части полученного сравнения на величину
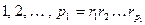 .
.
Тогда находим
 .
.
Отсюда имеем
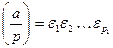 .
.
Далее рассмотрим величину
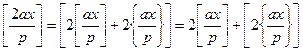 .
.
Величина слева будет четной или нечетной в зависимости от того, будет ли наименьший неотрицательный вычет числа 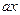 меньше или больше
меньше или больше  , т.е., будет ли
, т.е., будет ли 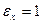 или
или 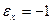 . Отсюда следует, что
. Отсюда следует, что
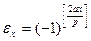
и
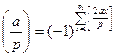 .
.
Предполагая 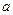 нечетным, преобразуем последнее равенство:
нечетным, преобразуем последнее равенство:

Тогда 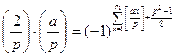 .
.
Теперь при 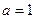 получаем искомую формулу. При этом для нечетного
получаем искомую формулу. При этом для нечетного 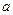 имеем
имеем
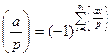 . (13.11)
. (13.11)
Следствие. 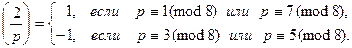
Результат легко проверяется непосредственно.
Теорема 13.16 (закон взаимности квадратичных вычетов).
Если  и
и 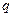 – различные простые нечетные, то
– различные простые нечетные, то
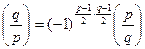 .
.
Следствие.
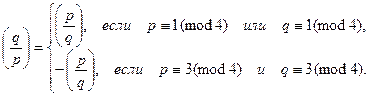
Здесь тоже легко проверяется выписанный результат.
Доказательство теоремы. Положим  и рассмотрим
и рассмотрим  пар чисел, получаемых, когда в выражениях
пар чисел, получаемых, когда в выражениях 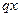 и
и 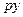 числа
числа 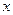 и
и  пробегают соответственно и независимо друг от друга системы значений:
пробегают соответственно и независимо друг от друга системы значений:
 ,
, 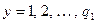 .
.
Не может быть такого, чтобы выполнялось равенство 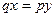 , потому что из этого равенства следовало бы, что
, потому что из этого равенства следовало бы, что 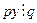 , но
, но  (последнее оттого, что
(последнее оттого, что 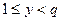 ). Поэтому положим
). Поэтому положим 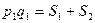 , где
, где  – число пар с
– число пар с 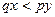 , а
, а 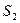 – число пар с
– число пар с  .
.
Легко заметить, что  есть число пар с
есть число пар с  . При этом нет противоречия с неравенством
. При этом нет противоречия с неравенством 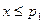 , так как из
, так как из 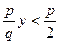 следует
следует  . Поэтому
. Поэтому
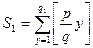 ,
,
Аналогично
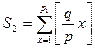 .
.
Применим формулу (13.11). Имеем
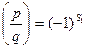 ,
, 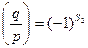 .
.
Поэтому
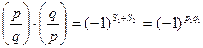 ,
,
что и требовалось.
Пример 13.25. Пусть надо вычислить 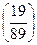 . Имеем
. Имеем
 .
.
Символ Якоби
Обобщением символа Лежандра является символ Якоби.
Определение 13.20. Пусть 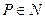 и нечетное,
и нечетное, 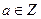 и
и 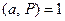 . Тогда символом Якоби называется арифметическая функция
. Тогда символом Якоби называется арифметическая функция 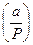 (читается «
(читается « 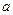 по
по  »), определяемая соотношением:
»), определяемая соотношением: 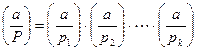 , где
, где  ,
, 
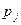 – простые числа,
– простые числа, 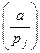 – символ Лежандра,
– символ Лежандра, 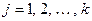 .
.
Этот символ можно использовать при вычислениях символа Лежандра. Отметим свойства символа Якоби, вытекающие из соответствующих свойств символа Лежандра.
1. 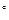
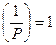 ;
;
2. 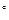
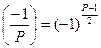 ;
;
3. 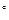
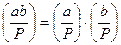 ;
;
4. 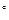
 ;
;
5. 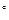
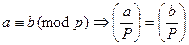 ;
;
6. 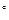
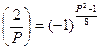 .
.
Доказательства этих свойств легко воспроизводятся на основании, как сказано, свойств символа Лежандра. Поэтому уделим внимание только свойствам 2 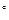 и 6
и 6 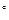 . Пусть
. Пусть  .
.
Доказательство свойства 2 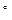 .
.
Имеем
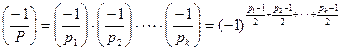 .
.
При этом
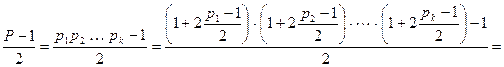
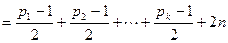 ,
, 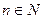 .
.
Отсюда и получается, что
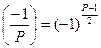 .
.
Доказательство 6 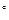 в известном смысле повторяет идею доказательства 2
в известном смысле повторяет идею доказательства 2 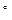 . Действительно,
. Действительно,
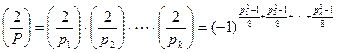 .
.
Но
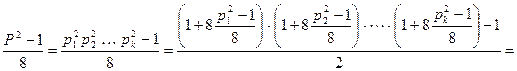
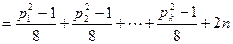 ,
, 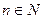 .
.
Тогда из предыдущей формулы находим, что
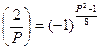 .
.
Похожим образом можно получить и закон взаимности для символов Якоби. 
Теорема 13.17 (закон взаимности символов Якоби).
Пусть  и
и 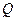 – натуральные взаимно простые нечетные числа. Тогда
– натуральные взаимно простые нечетные числа. Тогда
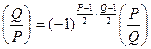 .
.
Доказательство. Пусть 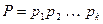 и
и 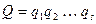 , где
, где 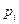 и
и 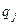 – простые числа,
– простые числа, 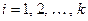 ,
, 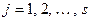 . Имеем
. Имеем
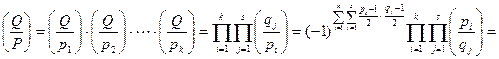
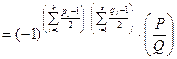 .
.
Далее, так же как и при доказательстве свойства 2 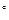 , находим
, находим
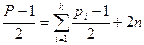 ,
, 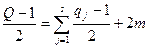 ,
, 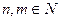 .
.
Поэтому в итоге получаем требуемое
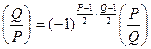 .
.
Пример 13.26. Пусть требуется узнать, является ли число 185 квадратичным вычетом по модулю 631. Вычислим символ Лежандра
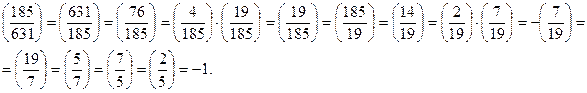
Результат вычислений показывает, что число 185 не является квадратом (квадратичным вычетом) по модулю 631.
Ясно, что число 185 не простое, тем не менее, символ можно «перевернуть» по теореме 13.17.

Первообразные корни и дискретный логарифм
Рассмотрим теперь мультипликативную группу классов вычетов. Пусть 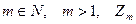 – кольцо классов вычетов по модулю
– кольцо классов вычетов по модулю  . Обозначим через
. Обозначим через  множество классов из
множество классов из  взаимно простых с
взаимно простых с  . Как уже отмечалось, такое подмножество существует как следствие свойства 14
. Как уже отмечалось, такое подмножество существует как следствие свойства 14  числовых сравнений.
числовых сравнений.
Лемма 13.28. Множество  относительно операции умножения классов образует мультипликативную группу порядка
относительно операции умножения классов образует мультипликативную группу порядка 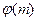 .
.
Доказательство. Учитывая теорему 13.7 требуется проверить обратимость классов. Действительно, пусть 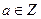 и
и 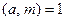 . Тогда по линейному представлению НОД (т. 13.2) получим, что для некоторых
. Тогда по линейному представлению НОД (т. 13.2) получим, что для некоторых 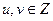
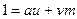 ,
,
откуда, переходя к классам, находим 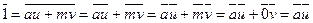 .
.
Таким образом, класс 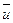 является обратным к классу
является обратным к классу 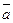 , т.е.,
, т.е., 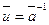 . Кроме того,
. Кроме того, 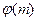 есть число классов взаимно простых с модулем
есть число классов взаимно простых с модулем  . Это доказывает лемму.
. Это доказывает лемму.
Определение 13.21. Пусть 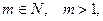
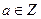 и
и 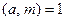 . Тогда наименьшее натуральное число
. Тогда наименьшее натуральное число 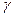 такое, что
такое, что  называется показателем, которому принадлежит
называется показателем, которому принадлежит 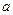 (или класс
(или класс 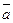 ) по модулю
) по модулю  .
.
Это определение имеет смысл хотя бы потому, что по теореме Эйлера 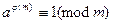 .
.
Лемма 13.29. Если показатель числа 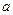 по модулю
по модулю  равен
равен 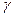 , то
, то 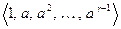 есть система чисел попарно несравнимых между собой по модулю
есть система чисел попарно несравнимых между собой по модулю  .
.
Доказательство. Если представить, что  , где
, где  , то легко находим, что
, то легко находим, что 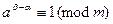 , где
, где 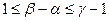 , а это противоречит определению показателя.
, а это противоречит определению показателя.
Лемма 13.30. Если показатель, которому принадлежит число 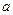 по модулю
по модулю  равен
равен 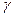 , то
, то 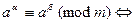
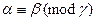 .
.
Доказательство. Разделим 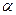 и
и 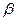 на число
на число 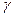 с остатком. Имеем
с остатком. Имеем
 ,
, 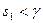 ,
,
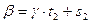 ,
, 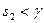 .
.
Необходимость. Из того, что 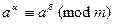 следует, что
следует, что 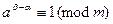 . Откуда
. Откуда
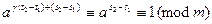 .
.
Так как 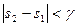 , то сравнение возможно лишь, если
, то сравнение возможно лишь, если 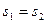 , т.е.,
, т.е., 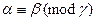 .
.
Достаточность. Если 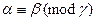 , то
, то 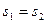 . Значит,
. Значит, 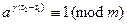 , а тогда
, а тогда 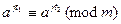 . Умножая обе части последнего сравнения на
. Умножая обе части последнего сравнения на  , где
, где  , получим, что
, получим, что  .
.
Следствие 1. 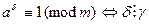 .
.
Следствие 2. 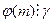 .
.
Последнее следствие приводит к определению, так как любой показатель обязательно делит число 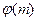 , и
, и 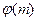 наибольший среди всех делителей.
наибольший среди всех делителей.
Определение 13.22. Если показатель, которому принадлежит число 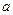 по модулю
по модулю  , равен
, равен 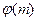 , то а называется первообразным корнем по модулю
, то а называется первообразным корнем по модулю  .
.
Из определения не ясно, существуют ли первообразные корни по модулю  . Докажем существование первообразных корней по модулям
. Докажем существование первообразных корней по модулям 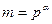 и
и  , где
, где  – простое нечетное. Но предварительно, рассмотрим два свойства показателей.
– простое нечетное. Но предварительно, рассмотрим два свойства показателей.
Дата добавления: 2019-07-26; просмотров: 617;
