Методы, основанные на теории возмущений

Один из наиболее удобных и часто используемых методов учета электронной корреляции – подход, основанный на теории возмущений. В основе этого подхода лежит поиск поправок к ВФ, найденной на основе приближенного метода (например, метода Хартри-Фока), которые учитывают корреляцию электронов. Наиболее часто используется вариант теории, называемый теорией возмущения Рэлея-Шредингера. В этом методе предполагается, что гамильтониан системы можно представить в виде суммы двух частей:

H = H₀ + λV

где H₀ – приближенный оператор, ВФ которого известны (или их легко найти), а V – оператор возмущения. Возмущением может быть любой физический процесс, характерная энергия которого мала по сравнению с энергией основного приближения, при этом т.е. одновременно должны быть равны нулю все коэффициенты при любых степенях λ:

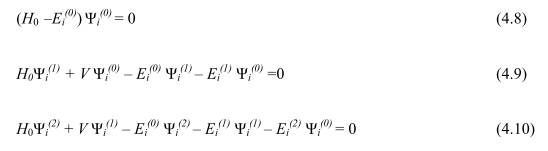
Особенность данной схемы в том, что для определения поправки к энергии степени (2n+1) достаточно знания поправки к ВФ только n-ной степени. Таким образом, чтобы определить поправку к энергии 2 и 3 порядков, достаточно знать поправку к ВФ только 1 порядка Ψi (1), причем она определяется как разложение по ВФ нулевого приближения. Начальным приближением может быть любая ВФ, достаточно точно описывающая рассматриваемую систему.

Поскольку расчет четвертой поправки проще расчета третьей, часто используется метод MP4(SDQ), в котором учитываются поправки только первого, второго и четвертого порядка. Отметим важную особенность методов, основанных на теории возмущений: получаемые в этом методе ВФ не являются вариационными, то есть нельзя оценивать качество получаемой ВФ по тому, насколько низка энергия системы. Кроме того, это означает, что нельзя сравнивать абсолютные значения энергии молекулы, полученные на разных уровнях теории возмущений.

Несмотря на вышеуказанный недостаток, теория возмущений является в настоящее время одним из наиболее точных и удобных инструментов квантовохимического исследования. Особенно это касается метода MP2, который требует значительно меньших вычислительных ресурсов, чем MP4, QCISD и CCSD, а его точность при определении молекулярной геометрии, энергии и колебательных частот во многих случаях вполне сравнима с этими прецизионными методами. Для метода MP2 разработаны весьма эффективные программы оценки градиента энергии, геометрической оптимизации и расчета частот. Проблемами теорий MPn являются системы с вырожденными открытыми оболочками, которые данным методом воспроизводятся неправильно. То же самое относится к возбужденным состояниям и молекулам, в состояниях, близких к диссоциации

Еще один пример принципиальной ошибки при расчете MP2 – неполный учет дисперсионной энергии при слабых межмолекулярных взаимодействиях. Поскольку теория MP2 учитывает только вклады корреляционной энергии до второго порядка включительно, ее точности совершенно не достаточно для правильного описания таких систем.