Метод конфигурационного взаимодействия

Рассмотрим более подробно метод конфигурационного взаимодействия и его современные варианты. Будем считать, что основная конфигурация Ф0 получена методом ХФР, а координаты электронов отличаются только пространственными компонентами.

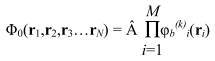
Здесь φi есть МО, выбранные в виде (3.7) в некотором базисе атомных орбиталей χj, j=1,L. Для наглядности рассмотрим пример, когда в системе имеется четыре МО, среди которых две дважды занятых (φ1, φ2) и две виртуальных (φ3, φ4):

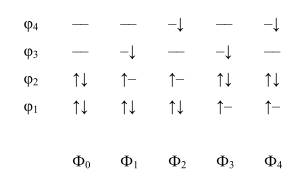
Способ построения волновой функции, соответствующей рис., называется методом КВ с однократными возбуждениями (Configuration Interaction with single excitations, CIS). Аналогично можно рассмотреть т.н. метод КВ с однократными и двойными возбуждениями (Configuration Interaction with single and double excitations, CISD). Для этого следует включить в (3.6) все конфигурации, рассмотренные на рис.4 и добавить к ним конфигурации, полученные путем переноса двух любых электронов с занятых МО основной конфигурации на любые свободные МО. Исключение составляет метод полного конфигурационного взаимодействия, ПКВ(Full CI,FCI), в котором учитываются все возможные расселения всех N электронов системы по всем имеющимся орбиталям системы. Для любой реальной системы это означает учет огромного числа однодетерминантных функций. Поэтому метод FCI применяется, как правило, только для простых систем в качестве эталонного метода, обладающего наивысшей точностью.

В ряде случаев основная конфигурация Ф0 обязана состоять из двух или нескольких детерминантов (быть многодетерминантной). Однако построение ряда КВ возможно и из многодетерминантных функций основного состояния. В этом случае получаемые волновые функции (3.6) называются многоссылочными(multireference wave functions, multireference CI) т.к. возбужденные конфигурации получены путем ссылок на несколько детерминантов основного состояния. Обычно при описании многоссылочных методов используется сокращение MR. Например, многоссылочный аналог метода CISD часто обозначается как MRSDCI.