Полуэмпирические методы

До сих пор описывались методы, рассматриваемые как «точные» в том смысле, что они выводятся путем дедукции из более общей строгой теории. Альтернативный подход предлагают полуэмпирические методы, в которых часть взаимодействий заменяется на подгоночные параметры, подбираемые на основе сравнения расчета некоторых реперных соединений и экспериментальных данных. В этом случае решение уравнения Шредингера может быть значительно упрощено, так, что это приводит к исключительно высокой вычислительной эффективности. Однако этот выигрыш достигается за счет меньшей строгости и, таким образом, возможной непредсказуемости результатов. Большинство полуэмпирических методов основываются на уравнениях Рутана. В этих уравнениях наибольшую сложность представляет расчет двухэлектронных молекулярных интегралов вида.

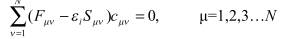
Эти интегралы возникают на этапе задания фокиана и должны пересчитываться на каждом шаге процедуры самосогласования. Для базиса с K функциями возникают K⁴/8 различных интегралов, которые далее должны быть преобразованы к системе молекулярных координат (т.н. «четырехиндексное преобразование», занимающее длительное время). Для системы большого размера (биомолекулы, многомолекулярные кластеры, фрагменты поверхности твердого тела) затраты на расчет интегралов становятся времяопределяющими. Один из путей решения это проблемы – сократить число учитываемых в расчете интегралов на основе т.н. приближения нулевого дифференциального перекрывания(НДП, zero differential overlap, ZDO). Оно состоит в том, что произведение всех различных орбиталей считается нулем:

φ_μ(r) φ_ν(r) = 0 для всех μ ≠ν (7.2)

Это более строгое предположение, чем просто S_μν = 0 для всех μ ≠ν (обычное условие ортогональности МО) и ведет к тому, что зануляются все двухэлектронные интегралы, за исключением (μμ|λλ). Число интегралов для расчета расчтет как K²/2, что гораздо меньше, чем в методе Хартри-Фока. Однако такое приближение имеет серьезные недостатки: (1) результаты становятся зависящими от поворота молекулы в пространстве (т.н. вращательная неинвариантность решения) и (2) пренебрежение перекрыванием между химически связанными атомами может привести к сильной недооценке ковалентного связывания.

Для решения первой проблемы - неинвариатности - предложено т.н. приближение ППДП, полное пренебрежение дифференциальным перекрыванием (complete neglect of differential overlap, CNDO), в котором интегралы (μμ|λλ) считаются независящими от типа орбиталей φ_μ и φ_λ, т.е. интегралы между орбиталями s-,p-, и d-типа считаются одинаковыми (при условии равенства показателей их орбитальных экспонент). Наиболее известную реализацию такого приближения представляет метод CNDO/2.В этом методе используются и другие приближения, например, в расчет включаются только валентные орбитали атома. Все интегралы между орбиталями одного атома оцениваются как постоянные параметры, величина которых находится из потенциалов ионизации атомов. В CNDO/2 и в большинстве других полуэмпирических методов, в отличие от неэмпирических методов и DFT, используется не гауссов, а слейтеровский базис атомных орбиталей, в котором радиальная часть атомной орбитали есть

φ_λ= a_λ rⁿ exp(-ζr)

Здесь a_λ есть нормировочный коэффициент, r - расстояние от ядра. Величина ζ (т.н. орбитальная экспонента) является подгоночным параметром, который, наряду с другими параметрами подбирается по экспериментальным данным. Кроме того, интегралы (μμ|λλ) между орбиталями одного атома также считаются постоянными параметрами и выбираются на основе воспроизведения потенциалов ионизации данного атома.

Исторически CNDO/2 был первым полуэмпирическим методом, который позволял проводить квантовохимическое исследование в его современном виде, в том числе оптимизацию молекулярной геометрии, расчет колебательных частот, расчет систем с открытыми оболочками, оценку потенциалов ионизации молекул, их дипольных моментов и т.д. Однако приближения, лежащие в его основе были слишком грубыми и предсказательная сила метода была невелика. Кроме того, он не был предназначен для оценки энергетики реакций и термодинамических свойств, поэтому к настоящему времени данный метод CNDO/2 практически вышел из употребления.

Несколько более последовательной схемой является приближение частичного пренебрежения дифференциальным перекрыванием, ЧПДП (intermediate neglect ofdifferential overlap, INDO). В этом подходе, в отличие от CNDO, учитываются те двухэлектронные интегралы, которые которые включают вклады орбиталей с различным спином. В результате пренебрежение дифференциальным перекрыванием применяется только к одноатомным интегралам, которые параметризуются на основе потенциалов ионизации атомных спектров. Точность метода INDO при расчетах геометрических и электронных параметрах молекул несколько лучше, чем CNDO/2, однако он обладает теми же недостатками - отсутствием термодинамической параметризации и низкой точности при расчете энергетических характеристик.

Частично эти недостатки были решены в модификации метода INDO – методе MINDO/3 (modified INDO, version 3), однако сегодня и его возможности не удовлетворяют современным требованиям. Расчеты этими методами имеет смысл проводить только тогда, когда в других, более современных методах отсутствует необходимая параметризация, или в качестве сравнения с результатами других методов. Одним из современных вариантов является схема ZINDO, преимущество которой состоит в том, что она тщательно параметризована для воспроизведения данных электронной спектроскопии, включает в себя термодинамическую параметризацию, и, что наиболее ценно, позволяет рассчитывать соединенияпереходных элементов.

Наиболее последовательной полуэмпирической схемой на сегодняшний день является приближение пренебрежения двухатомным дифференциальным перекрыванием(neglect of diatomic differential overlap, NDDO). В этом приближении условие (7.2) накладывается только на те орбитали μ и ν, которые принадлежат различным атомам. Это приводит к тому, что обращаются в ноль только трех- и четырехцентровые интегралы (μν|λσ), При этом в большинстве расчетных схем, основанных на этом приближении, одноцентровые интегралы по-прежнему оцениваются из спектроскопических данных, а для расчета двухцентровых интегралов используются приближенные методы, основанные на мультипольном разложении межэлектронного потенциала. В результате время расчета по сравнению с неэмпирическими методами резко сокращается, а точность остается вполне сопоставимой с ними.

Наиболее известны три метода, основанных на приближении NDDO: MNDO, PM3, AM1. Параметры методов MNDO, AM1 и, особенно, PM3 тщательно подобраны по экспериментальным данным, включающим длины связи, валентные и двугранные углы, энтальпии образования, дипольные моменты и потенциалы ионизации молекул. Причем в случае PM3 использовался набор из более чем 400 реперных соединений. Все это приводит к тому, что точность этих расчетных схем значительно выше, чем их предшественников, практически для всех рассматриваемых величин. Следует отметить, что хотя метод MNDO достаточно плохо описывает межмолекулярные невалентные взаимодействия, методы AM1 и PM3 специально параметризованы для описания систем с водородными связями и донорно-акцепторных комплексов (эти системы были включены в реперные наборы при оптимизации параметров). Наиболее же важное преимущество полуэмпирических методов - их высокая вычислительная эффективность, причем время расчета часто в десятки и сотни раз меньше, чем в случае неэмпирических методов и даже ТФП. Это позволяет проводить расчеты очень больших молекул, таких как белки, нуклеиновые кислоты, фрагменты поверхности твердого тела, капли жидкости. В ряде случаев эти методы используются в современных вариантах «составных методов» типа (ONIOM), в которых внешняя мультимолекулярная часть сложной системыописывается грубым методом, в то время как внутренняя (наиболее важная и небольшая по размеру) рассчитывается более точным неэмпирическим методом.

К сожалению, принципиальным недостатком данного типа методов является ихнизкая предсказательная сила в случае неклассических соединений, что связано с подбором их параметров по ограниченному набору соединений. Как следствие, эти методы дают хорошие результаты при расчете тех классов соединений, которые были включены в реперный набор.

Еще один недостаток полуэмпирических методов - отсутствие атомных параметров для многих элементов таблицы Менделеева. Поскольку для подбора параметров требуются надежные экспериментальные данные по структуре, термохимии и электронным характеристикам газофазных молекул, эта процедура для многих элементов невозможна.

Следует также помнить, что исходные варианты методов MNDO, AM1, PM3 использовали схему расчета двухэлектронных интегралов, которая с большим трудом распространяется на орбитали d- и f- типа. Современные варианты этих методов, в которые часто включаются и переходные элементы, используют иные схемы расчета.

Подытоживая сказанное, отметим, что с развитием вычислительной техники полуэмпирические методы в их вышеописанных вариантах постепенно вытесняются методами ab initio и ТФП, прежде всего, вследствие их низкой предсказательной силы при расчетах молекул неклассического строения. Сегодня их область применения ограничена большими системами - биомолекулами, кластерами и супрамолекулярными системами, причем в тех случаях, когда требуется получение только качественных или полуколичественных результатов. Кроме того, иногда их удобно применять для выбора стартовой точки при оптимизации неэмпирическими методами. Однако и в этом случае следует помнить, что часто такая процедура приводит к худшим результатам (к более длительной оптимизации или получению принципиально неверных структур), чем даже при выборе начальной структуры «на глаз». Последнее особенно относится к поиску переходных состояний, в котором использование результатов полуэмпирических методов в качестве стартовой точки, как правило, приводит к неправильным результатам.

В ряде случаев, однако, результаты полуэмпирических схем и сегодня оказываются предпочтительнее, чем результаты неэмпирических методов. Например, это имеет место при расчетах магнитнорезонансных параметров молекул, а также расчетах электронновозбужденных состояний методом ZINDO, особенно в случаемолекул с атомами переходных элементов.