Метод связанных кластеров и родственные методы

Полное КВ разложение было бы чрезвычайно трудоемким, из-за огромного числа коэффициентов C_abcd^rtsu. Однако можно предположить, что эти коэффициенты в действительности не являются независимыми. Например, можно предположить, что коэффициенты четвертичных возбуждений являются комбинациями коэффициентов двойных возбуждений:

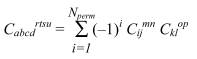
Эта идея является основой т.н. метода связанных кластеров с двойными возбуждениями(Coupled Cluster method with Double excitations, CCD). Это соотношение позволяет получить более точное приближение многоэлектронной ВФ, чем ПНП. Получающийся метод является одновременно размерно согласованным и инвариантным относительно унитарных преобразований. Идея, изложенная выше, может быть обобщена на произвольные кластеры. Для этого вводится т.н. кластерный оператор T:

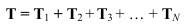
где действие оператора Ti обозначает получение всех i-кратно возбужденных детерминантов, действующих на референсную многоэлектронную функцию. Многоэлектронная ВФ может быть записана как

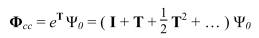
Это разложение можно подставить в электронное уравнение Шредингера чтобы получить значения кластерных амплитуд. Чаще всего ряд (5.4) ограничивают только несколькими первыми слагаемыми, например, T = T₁ + T₂ , что соответствует одно- и двукратным возбуждениям. Это соответствует методу связанных кластеров с одно- и двукратными возбуждениями (Coupled Cluster method with Single and Double excitations, CCSD), причем Ψ₀ - референсная ВФ, получаемая методом Хартри-Фока (ОХФ или НХФ, в зависимости от типа рассматриваемой системы).

С целью ускорения расчета можно комбинировать методы связанных кластеров и теории возмущений. Например, вклады тройных возбуждений, явный учет которых в методе связанных кластеров приводит к значительному усложнению расчета, можно учитывать методом MP4 и затем прибавлять к энергии CCSD. Такой метод, называемый CCSD(T), является сегодня одним из наиболее часто используемых.

Метод связанных кластеров оценивает корреляционную энергию очень точно и сегодня рассматривается как один из наиболее точных подходов квантовой химии. Точность расчета энергий реакций в большинстве случаев сравнима с точностью лучших экспериментальных методов.

Следует, однако, помнить, что точность метода связанных кластеров сильно зависит от выбора базиса атомных орбиталей и корректный учет корреляционной энергии не может быть проведен в базисах малого и среднего размера. Как правило, для этих целей используются специальные корреляционно-согласованные базисы (ccpV_xZ) и базисы с поляризационными функциями высших угловых моментов.

Недостатком метода связанных кластеров является его очень высокая трудоемкость. Время вычисления в методах CCD и CCSD растет как N⁶ (N – число электронов), а в варианте CCSD(Т) - как N⁸. Такие затраты приводят к тому, что расчеты методом связанных кластеров на персональных компьютерах возможны пока только для молекул небольшого размера (до 10 атомов), для расчетов больших молекул требуется использование высокопроизводительных компьютерных систем.

Кроме того, следует всегда помнить, что методы связанных кластеров являются примером односсылочного метода. Поэтому, хотя динамическая корреляция учитывается на том уровне весьма точно, результаты расчета для любой системы с электронным вырождением будут неправильными.

В качестве разновидности метода связанных кластеров можно рассматривать т.н. метод квадратичного КВ (quadratic configuration interaction method, QCI), в его вариантах с двухкратными и неявными трехкратными возбуждениями QCISD, QCISD(T), а также метод бракнеровских пар(BDSD) Хотя эти методы создавались независимо от метода связанных кластеров, их волновые функции могут быть представлены в виде, сходном с (5.6). Различия между этими методами заключаются в различном учете первых членов разложения (5.6), однако более последовательной и полной является теория связанных кластеров, изложенная выше.