Неограниченный метод Хартри-Фока

Ограниченный Метод Хартри-Фока нельзя применять для систем с открытыми (незамкнутыми)оболочками: радикалы (один неспаренный электрон), триплетные и синглетные возбужденные состояния молекул (два неспаренных электрона), многие органические и неорганические комплексы переходных металлов (несколько неспаренных электронов, заселяющих вырожденные d- или f-орбитали), изолированые атомы с незаполненными оболочками. Метод нахождения волновой функции, аналогичный методу ОХФ, при котором пространственные части одноэлектронных спин-орбиталей варьируются независимо, называется неограниченным методом Хартри-Фока (НХФ, UHF).

Получаемые выражения для оператора Фока и энергии сходны с выражениями ограниченного метода ХФ, однако уравнения Хартир-Фока-Рутана распадаются на две части, соответствующие электронам с противоположными спинами:

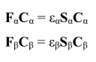
Процедура самосогласования остается аналогичной методу ОХФ, однако получаемые решения имеют особенности, отличающие их от решений ОХФ.

1) Коэффициенты МО электронов с разными спинами С_ij^α и С_ij^β не одинаковы.

2) Когда количества электронов с противоположными спинами не равны, различными оказываются и энергии спин-орбиталей ε_α и ε_β.

Главными преимуществами метода НХФ является возможность описания систем с неспаренными электронами и его простота, поскольку алгоритм расчета, как и структура программ, аналогичны методу ОХФ. В настоящее время, подавляющее большинство квантовохимических программ включают модули, позволяющие находить решения методом НХФ. Недостатки метода НХФ:

Принципиальная невозможность расчета систем в вырожденных электронных состояниях. Вариация пространственных частей спин-ориталей, проводимая в данном методе без ограничений, может привести к тому, что ВФ перестанет иметь строго определенное значение полного спина. В результате полный спин решения может принимать физически абсурдные значения (0.76, 0.8). С целью устранения вышеуказанного недостатка часто используют т.н. спин-проектированные методы НХФ (P-HF, projected Hartree Fock method), в котором решение, полученное обычным способом, подвергается проектированию на ВФ, точно соответствующую заданному значению спина. Он также часто является основой методов учета электронной корреляции в системах с открытой оболочкой (MPn, QCISD и CCSD). Применение идей метода НХФ возможно (и часто используется) и в рамках теории функционала плотности.

Метод ОХФО

Системы с открытыми оболочками (радикалы, триплетные состояния и т.д.) часто описываются однодетерминантным методом НХФ. Как обсуждалось выше, его недостаток состоит в том, что волновая функция в этом случае не является собственной функцией оператора полного спина. Другая проблема появляется тогда, когда требуется сравнить энергии и другие свойства системы с замкнутой оболочкой и родственных ей систем с открытыми оболочками. В методе НХФ часто не удается прийти к решению, отличному от решения ОХФ вблизи равновесной геометрии молекулы. Это означает, что мы описываем систему с замкнутой оболочкой, применяя дважды занятые орбитали.

Эти и сходные проблемы частично удается решить с помощью т.н. «ограниченного метода Хартри-Фока для открытой оболочки» (ОХФО, Restricted Open-shell Hartree-Fock method, ROHF), в котором замкнутые и открытые оболочки описываются по-разному. Замкнутые оболочки состоят из дважды занятых орбиталей; их расщепление не предполагается. В зависимости от природы открытой оболочки, волновая функция может быть одним детерминантом, как в случае дублета или высокоспиновых компонент триплета (Sz = 1 или Sz = –1) , или же может быть линейной комбинацией двух или более детерминантов. В схеме ОХФО разные системы открытых оболочек описываются по единой схеме на основе достаточно общего выражения для энергии, содержащего численные коэффициенты, значения которых отличаются для разных задач. Во всех случаях предполагается, что мы имеем дело с некоторым числом N ортонормированных (пространственных) орбиталей (φi, каждой из которых можно сопоставить свое число заполнения ωi, и тогда электронную энергию можно записать как:

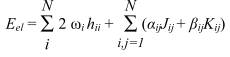
где «коэффициенты связи» αij и βij определяются типом состояния с открытой оболочкой (т.е. для каждого типа открытой оболочки – дублета, триплета и т.д. выбираются соответствующие константы α и β). Для определения ВФ используется обычная процедура вариации электронной энергии (2.64) с использованием метода множителей Лагранжа, однако в результате вариации получаются уравнения Эйлера. Система этих уравнений распадается на совокупность N уравнений т.н. «k-зависи­мых» операторов Фока ОХФО, т.е. для каждой орбитали или каждого класса орбиталей имеется свой оператор Фока:

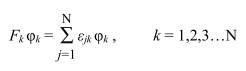
Часто удобнее записать систему уравнений в виде одного уравнения. Чтобы это сделать, вводят т.н. единый связывающий оператор (unified coupling operator), который объединяет все уравнения, причем получаемые затем уравнения оказываются идентичны уравнениям Хартри-Фока и решаются аналогичным образом путем самосогласования.

В целом метод ОХФО дает более правильное описание ВФ открытых систем, чем метод НХФ, поскольку его ВФ изначально обладает правильной спиновой симметрией. Исключение составляют явления спиновой поляризации, о которых говорилось в начале раздела. Наибольшее преимущество этот метод демонстрирует при описании вырожденных и высокоспиновых систем, для которых НХФ и другие методы, за исключением КВ и МК ССП, непригодны.

Недостатками данного метода является необходимость «ручного» задания коэффициентов ωi, αij, βij для различных типов вырожденных состояний а также то, что большинство используемых программ использует единые связывающие операторы, не воспроизводящие теорему Купманса. Точность оценки многих молекулярных свойств в случае низкоспиновых и неврожденных открыто оболочечных систем (радикалы, невырожденные триплеты), а также систем с замкнутыми оболочками не может конкурировать с точностью методов MPn, DFT, CCSD и QCISD.