Основные приближения

Рассмотрим изолированную молекулу, не испытывающую внешних воздействий. Для ее описания используем следующую модель:

1. Учитывается только притяжения электронов к ядрам и отталкиванием электронов друг от друга;

2. Состояние молекулы стационарно (ее энергия E не зависит от времени);

3. Ядра атомов неподвижны и их координаты Rточно определены (адиабатическим приближением).

С учетом сделанных предположений, волновая функция молекулы Ψ зависит только от координат электронов и подчиняется стационарному уравнению Шредингера:

ĤΨ(r) = EΨ(r)

Поскольку мы пренебрегли всеми взаимодействиями, за исключением взаимодействием электронов с ядрами и электронов друг с другом, гамильтониан молекулы Ĥ включает только три члена: кинетическую энергию электронов, притяжение электронов к ядрам атомов и отталкивание электронов между собой. Тогда гамильтониан молекулы есть сумма двух членов

Ĥ= ĥ +Ĝ (2.2)

Однако поведение системы электронов зависит от того, в каком спиновом состоянии находится каждый из них. Пусть отдельный (например, изолированный) электрон i описывается волновой функцией φ:

φ = φ(r_i,σ_i)

Здесь r_i - пространственные (например, декартовы) координаты электрона i, σ_i - его спиновая переменная. Т.к. проекция спина электрона s_z может принимать только два значения (+ħ/2 и –ħ/2), то спиновая переменная также принимает только два значения (назовем их, соответственно, α и β).

Сделаем еще одно предположение, которое, строго говоря, является приближением: допустим, что спин и пространственные переменные независимы и волновую функцию отдельного электрона можно представить в виде произведения двух независимых функций:

φ(r,σ) = φ(r)η_ς(σ) (2.7)

Здесь η_ς(σ) - спиновая волновая функция электрона со спином ς , т.е. волновая функция, определяющая вероятность обнаружить данный электрон со спином σ=ς. Мы не знаем явный вид этой функции, но очевидно, что она может принимать только строго определенные значения.

φ(r_i)η_iα(σ) → φ(i)α(i) (2.8)

φ(r_i)η_iβ(σ) → φ(i)β(i) (2.9)

Смысл записи (2.8) состоит в том, что пространственная вероятность обнаружения электрона i описывается квадратом модуля функции φ_i(r), а его проекция спина в этом состоянии +1/2ħ (т.е. α). Одноэлектронные волновые функции вида (2.7), являющиеся решением молекулярного уравнения Шредингера, называются спин-орбиталями, а их пространственные компоненты φ(r) - одноэлектронными орбиталямимолекулы.

С учетом сделанных обозначений стационарное уравнение Шредингера (2.1) следует записать в виде:

ĤΨ(q₁, q₂, … q_N) = EΨ(q₁, q₂, … q_N) (2.10)

где q_i=(r_i,σ_i) - совокупность пространственных и спиновых переменных электрона i. Вид оператора Ĥ при этом совершенно не изменяется, и он по-прежнему действует только на пространственные координаты электронов. Спиновая часть волновой функции является для операторов ĥ и Ĝ просто постоянным множителем, который можно вынести за скобки. Эта часть, однако, будет иметь значение при проведении интегрирования по всем координатам электронов, включая спиновые переменные.

Наша задача состоит в нахождении волновой функции Ψ(q₁, q₂, … q_N) из уравнения (2.10), в котором гамильтониан Ĥ задан формулами (2.2)-(2.5). Это уравнение является 3N-мерным дифференциальным уравнением второго порядка в частных производных, решение которого требует дальнейших упрощений.

Важное приближение, позволяющее значительно упростить уравнение (2.10) было предложено английским физиком Д. Хартри. Многоэлектронная волновая функция Ψ(q₁, q₂, … q_N) представляет собой произведение функций, зависящих от координат только одного электрона:

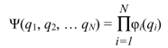
Оно соответствует системе, в которой все электроны движутся независимо друг от друга, что в случае молекулы, конечно же, неверно. Приближение Хартри также не подчиняется принципу Паули, который гласит, что волновая функция, описывающая состояния электронов, должна менять знак при перестановке координат любых двух электронов. Выход из этой ситуации был предложен советским физиком В.А. Фоком и одновременно американским физиком Дж. Слейтером: необходимо подействовать на функцию специальным оператором (т.н. оператором антисимметризацииA), который превращает любое произведение функций в антисимметричную относительно перестановки двух электронов.

В соответствие с физическим смыслом волновой функции на функцию (2.15) должно быть наложено еще одно физическое условие - условие нормировки:

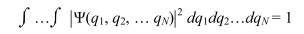
которое означает, что вероятность обнаружить любой из N электронов молекулы во всем пространстве с любым спином равна 1.