Ограниченный метод Хартри-Фока. Уравнения Рутана.

До сих пор развиваемая теория оставалась общей в том смысле, что не зависела от типа рассматриваемых молекул. Если считать, что в молекуле четное число электронов и число электронов со спином α равно числу электронов со спином β, т.е. N_α/2 = N_β/2 = n. Кроме того, предположим, что все электроны спарены, т.е. пары электронов занимают одну и ту же пространственную орбиталь, различаясь только спином. Качество этого приближения ухудшается при растяжении связей и, наконец, нарушается при диссоциации связи, когда электронам энергетически выгоднее находиться в неспаренном состоянии. Такой тип молекул в действительности очень распространен и называется молекулами с замкнутыми (закрытыми) электронными оболочками. Тогда уравнения Хартри-Фока сводятся к более простому виду:

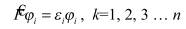
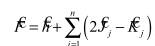
Уравнение Хартри-Фока, в принципе, позволяет найти волновые функции многоэлектронной системы, однако в случае молекул его прямое решение все еще оказывается весьма сложным. Для описания молекулярных систем требуется сделать дополнительные упрощения. Будем искать одноэлектронные функции многоэлектронной системы в виде линейной комбинации одноэлектронных функций центрированных на ядрах атомов (атомных орбиталей). Это приближение называется приближением "Молекулярная Орбиталь – Линейная Комбинация Атомных Орбиталей", или МО-ЛКАО.

Тогда можно показать, что выражение (2.46) можно представить в виде системы линейных уравнений (уравнения Рутана):

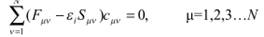
или в матричном виде:

FC=SCε,(2.51)

Здесь матрица F- т.н. оператор Фока(фокиан).Матрица Pназывается матрицей плотности, S –называются интегралами перекрывания, χ_i - базисные функции, центрированные на ядрах атомов, r- векторы пространственных координат электронов. Величины ε_i называются одноэлектронными энергиями или энергией молекулярной орбиталиi. Можно показать, что энергия МО с точностью до знака равна энергии удаления электрона с данной МО (т.е. потенциалу ионизации с данной МО) при условии, что орбитали системы в ходе этого процесса рассматриваются как неизменные (Теорема Кумпанса).

IP_i = -ε_i (2.56)

Решение уравнения Рутана (2.51) генерирует набор коэффициентов c_ij, которые являются коэффициентами разложения молекулярной орбитали φ_i (r_i)по базисным функциям (атомным орбиталям) χ (r_i).

Однако, уравнения Рутана имеют еще одну сложность - фокиан зависит от матрицы плотности, которая, в свою очередь определяется через c_ij - т.е. через решения самих уравнений Рутана. Чтобы выйти из этого заколдованного круга, В.А. Фок предложил решать уравнения (2.48) с помощью итерационной процедуры, которая получила название процедуры самосогласования. Сам метод Хартри-Фока часто называют методом самосогласованного поля (ССП). В соответствие с этой процедурой вначале выбирается некая приближенная матрица плотности и формируется начальный фокиан. Затем решаются уравнения (2.51) и находится новая (уже более точная) матрица плотности.

Процессу самосогласования посвящено большое количество специальных научных исследований. В настоящее время выработаны специальные алгоритмы (конвергеры), позволяющие ускорить сходимость процедуры ССП или добиться самосогласования для систем с плохой сходимостью. Наиболее простым методом является сдвиг виртуальных орбиталей на некоторую энергию dE вверх, так, что энергетическая щель между занятыми и виртуальными орбиталями увеличивается. Более сложным способом являются известные и часто применяемые процедуры DIIS и SOSCF, которые во многих случаях дают более высокое ускорение сходимости. Большинство современных квантовохимических программ позволяет произвольно использовать тот или иной конвергер по желанию пользователя. Следует, однако, помнить, что до настоящего времени нет универсальной процедуры, гарантирующей сходимость процедуры самосогласования во всех случаях.