АРИФМЕТИКА. Теория делимости 3 страница
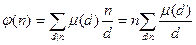 .
.
Ввиду того, что функция под знаком суммы мультипликативна, то по лемме 13.12. 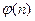 тоже мультипликативна.
тоже мультипликативна.
Следствие. По лемме 13.13. получаем
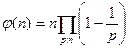 ,
,
где произведение распространено на все простые делители числа  .
.
Теорема 13.6 (соотношение Гаусса).
Имеет место формула 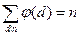 .
.
Доказательство. В силу мультипликативности 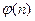 в соответствии с леммой 13.13 получим
в соответствии с леммой 13.13 получим
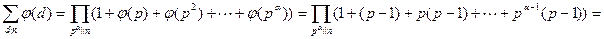
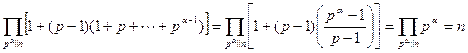 .
.
Здесь обозначение 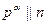 значит, что
значит, что 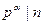 , но
, но 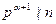 , т.е., «точное» деление на
, т.е., «точное» деление на  .
.
Числовые сравнения
Введем специальное бинарное отношение на множестве целых чисел.
Определение 13.12. Пусть 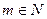 и
и  . Тогда говорят, что два целых числа
. Тогда говорят, что два целых числа  и
и 
сравнимы по модулю  , если
, если 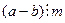 . Обозначение:
. Обозначение: 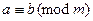 . Числа
. Числа  и
и  называются соответственно левой и правой частью сравнения.
называются соответственно левой и правой частью сравнения.
Лемма 13.19. Если 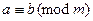 , то числа имеют одинаковые остатки при делении на число
, то числа имеют одинаковые остатки при делении на число  , т.е., являются равноостаточными. Равноостаточность является одновременно и признаком сравнимости.
, т.е., являются равноостаточными. Равноостаточность является одновременно и признаком сравнимости.
Доказательство. Тривиальное.
Лемма 13.20. Условие сравнимости 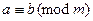 эквивалентно условию
эквивалентно условию 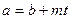 , где
, где 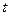 есть некоторое целое число.
есть некоторое целое число.
Доказательство. Тривиальное.
Лемма 13.21. Бинарное отношение сравнимости на множестве всех целых чисел является отношением эквивалентности.
Доказательство. Очевидно, что 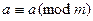 и если
и если 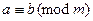 , то
, то 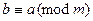 . Поэтому докажем транзитивность отношения. Пусть
. Поэтому докажем транзитивность отношения. Пусть 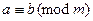 и
и 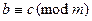 , тогда по лемме 13.20
, тогда по лемме 13.20 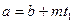 и
и 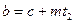 для некоторых
для некоторых 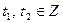 . Отсюда получаем, что
. Отсюда получаем, что
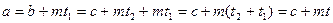 ,
, 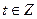 .
.
Значит, 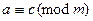 .
.
Рассмотрим свойства числовых сравнений. Пусть 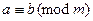 и
и 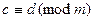 . Тогда
. Тогда
1. 
 ;
;
2. 
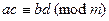 ;
;
3. 
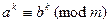
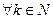 ;
;
4. 
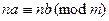
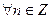 ;
;
5. 
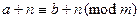
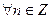 ;
;
6.  Числа из одной части сравнения можно переносить в другую часть с изменением знака. Так, если
Числа из одной части сравнения можно переносить в другую часть с изменением знака. Так, если 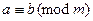 , то
, то 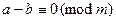 ;
;
7.  Если
Если 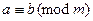 ,
,  и
и 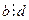 причем
причем  , то
, то 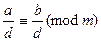 ;
;
8.  Если
Если 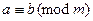 , то
, то 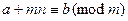
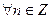 ;
;
9.  Если
Если 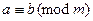 , то
, то 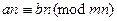
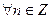 ;
;
10.  Если
Если 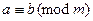 и
и  ,
, 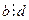 ,
, 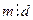 , то
, то 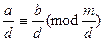 ;
;
11.  Если
Если  и
и 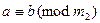 , то
, то 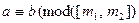 ;
;
12.  Если
Если 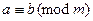 , то
, то 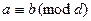
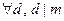 ;
;
13.  Если какая-то часть сравнения и модуль делятся на некоторое число, то другая часть должна делиться на это число.
Если какая-то часть сравнения и модуль делятся на некоторое число, то другая часть должна делиться на это число.
14.  Если
Если 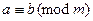 , то
, то 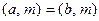 .
.
Доказательства этих свойств достаточно простые, основанные на определении и леммах 13.19 и 13.20. Докажем, например, свойство 7  . Если
. Если 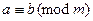 ,
,  и
и 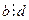 , то
, то 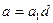 ,
, 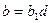 . Значит,
. Значит, 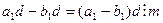 . Тогда по первому свойству взаимно простых чисел, так как
. Тогда по первому свойству взаимно простых чисел, так как  ,
, 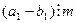 , т.е.,
, т.е., 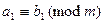 , что и требовалось.
, что и требовалось.
Вновь пусть 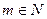 и
и  . По лемме 13.21 бинарное отношение сравнимости есть отношение эквивалентности на множестве
. По лемме 13.21 бинарное отношение сравнимости есть отношение эквивалентности на множестве 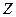 , поэтому это множество распадается на классы эквивалентности, т.е., на классы сравнимых между собой чисел. В силу леммы 13.19 таких классов будет ровно
, поэтому это множество распадается на классы эквивалентности, т.е., на классы сравнимых между собой чисел. В силу леммы 13.19 таких классов будет ровно  , ибо при делении на число
, ибо при делении на число  будет ровно такое количество различных остатков.
будет ровно такое количество различных остатков.
Определение 13.13. Элемент класса эквивалентности по модулю  называется вычетом по модулю
называется вычетом по модулю  .
.
Таким образом, можно говорить о классах вычетов по модулю  . Введем обозначение. Класс чисел, содержащий остаток
. Введем обозначение. Класс чисел, содержащий остаток 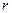 обозначим через
обозначим через 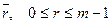 . И рассмотрим множество таких классов, которое обозначим через
. И рассмотрим множество таких классов, которое обозначим через 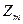 . Именно
. Именно
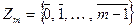 .
.
На множестве 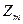 введем две бинарные алгебраические операции: сложение классов и их умножение.
введем две бинарные алгебраические операции: сложение классов и их умножение.
Пусть для любых 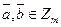
 и
и  . Черта над суммой и произведением означает эти числа заменяются на соответствующие остатки от деления на
. Черта над суммой и произведением означает эти числа заменяются на соответствующие остатки от деления на  . Надо сказать, что любое число из класса вычетов может представлять этот класс. При этом операции, представленные выше, определены корректно. В самом деле, пусть
. Надо сказать, что любое число из класса вычетов может представлять этот класс. При этом операции, представленные выше, определены корректно. В самом деле, пусть 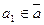 ,
, 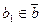 , т.е.,
, т.е., 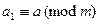 ,
, 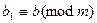 . Тогда по первому свойству сравнений получаем, что
. Тогда по первому свойству сравнений получаем, что 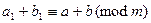 . А это значит, что
. А это значит, что 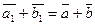 . Таким образом, сумма классов не зависит от выбора представителей классов. Аналогично и
. Таким образом, сумма классов не зависит от выбора представителей классов. Аналогично и 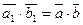 на основе второго свойства сравнений.
на основе второго свойства сравнений.
Теорема 13.7. Тройка  есть коммутативное кольцо с единицей.
есть коммутативное кольцо с единицей.
Доказательство. В совокупности аксиом об аддитивной группе кольца можно утверждать, что операция алгебраична и ассоциативна. Последнее следует из выкладки:
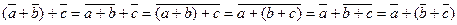
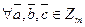 .
.
По аналогии доказывается коммутативность сложения. Нейтральным элементом будет класс  , а противоположным для
, а противоположным для 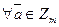 является класс
является класс  .
.
Операция умножения также алгебраична и ассоциативна. В предыдущей выкладке стоит лишь заменить знак сложения на знак умножения. Умножение также коммутативно. Роль единицы играет класс 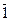 . Остается проверить выполнимость дистрибутивного закона. Имеем
. Остается проверить выполнимость дистрибутивного закона. Имеем
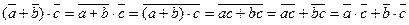
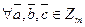 .
.
Теорема доказана.
Следствие 1. Если  – число составное, то кольцо имеет делители нуля. В самои деле, если
– число составное, то кольцо имеет делители нуля. В самои деле, если 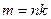 , где
, где 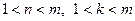 ,
, 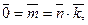 но
но 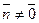 и
и 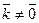 .
.
Следствие 2. Если  – простое, то
– простое, то 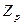 – поле, называемое полем классов вычетов.
– поле, называемое полем классов вычетов.
Действительно, если 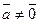 , то
, то 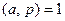 . Значит, по линейному представлению НОД получим, что для некоторых целых
. Значит, по линейному представлению НОД получим, что для некоторых целых 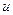 и
и 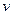
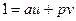 . На языке классов это означает, что
. На языке классов это означает, что
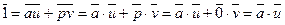 ,
,
т.е., обратным к ненулевому классу 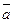 оказывается класс
оказывается класс 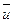 . Что и требовалось. Это доставляет пример конечного поля.
. Что и требовалось. Это доставляет пример конечного поля.
Пример 13.16. Пусть 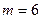 . Зададим таблицы Кэли для операций в кольце
. Зададим таблицы Кэли для операций в кольце 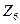 . Для простоты записи откажемся от черточек при изображении классов.
. Для простоты записи откажемся от черточек при изображении классов.
| * | ||||||
| + | ||||||
Определение 13.14. Система чисел, взятых по одному из каждого класса вычетов по модулю  , называется полной системой вычетов по модулю
, называется полной системой вычетов по модулю  (ПСВ).
(ПСВ).
Пример 13.17. Пусть 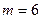 , тогда системы
, тогда системы
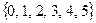 и
и 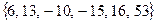
являются полными системами вычетов по модулю 6.
Обычно используются системы наименьших неотрицательных вычетов, а также системы вычетов наименьших по абсолютной величине. Именно по модулю  соответственно:
соответственно:
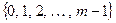
и при 
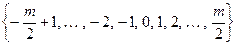 или
или 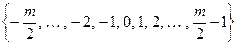 ,
,
при 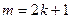
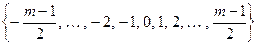 .
.
Лемма 13.22. Любая система  целых чисел попарно не сравнимых между собой по модулю
целых чисел попарно не сравнимых между собой по модулю  образует полную систему вычетов по модулю
образует полную систему вычетов по модулю  .
.
Доказательство. Очевидно.
Лемма 13.23. Если 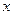 пробегает ПСВ по модулю
пробегает ПСВ по модулю  , то
, то 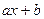 тоже пробегает ПСВ по модулю
тоже пробегает ПСВ по модулю  , если
, если 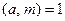 , при любом целом
, при любом целом 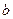 .
.
Доказательство. Ясно, что указанное выражение принимает  значений. Эти значения попарно не сравнимы между собой по модулю
значений. Эти значения попарно не сравнимы между собой по модулю  . Действительно, если при
. Действительно, если при 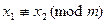 тем не менее
тем не менее 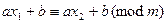 , то тогда
, то тогда 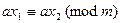 . Так как
. Так как 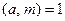 , то по свойству 7
, то по свойству 7  сравнений получили бы
сравнений получили бы 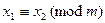 , что приводит к противоречию. Значит, на основе предыдущей леммы заключаем, что
, что приводит к противоречию. Значит, на основе предыдущей леммы заключаем, что 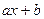 тоже пробегает ПСВ по модулю
тоже пробегает ПСВ по модулю  .
.
Легко видеть, что числа одно класса вычетов по модулю  имеют один и тот же НОД с
имеют один и тот же НОД с  (свойство 14
(свойство 14  сравнений). Поэтому, если такой НОД равен единице, то можно
сравнений). Поэтому, если такой НОД равен единице, то можно
говорить о классе вычетов взаимно простом с модулем.
Определение 13.15. Система чисел, взятых по одному из каждого класса вычетов по модулю  взаимно простого с
взаимно простого с  , называется приведенной системой вычетов по модулю
, называется приведенной системой вычетов по модулю  (ПрСВ).
(ПрСВ).
Приведенную систему вычетов можно составить из вычетов полной системы, взяв из нее только те вычеты, которые взаимно просты с модулем. Например, из системынаименьших неотрицательных вычетов. Тогда становится ясным, что количество чисев в ПРСВ по модулю  равно
равно 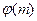 .
.
Пример 13.18. Если 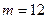 , то ПрСВпо модулю 12 есть
, то ПрСВпо модулю 12 есть 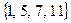 .
.
Лемма 13.24. Система 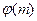 целых чисел попарно не сравнимых между собой по модулю
целых чисел попарно не сравнимых между собой по модулю  и взаимно простых с
и взаимно простых с  образует приведенную систему вычетов по модулю
образует приведенную систему вычетов по модулю  .
.
Доказательство. Очевидно.
Лемма 13.25. Если 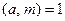 и
и 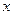 пробегает приведенную систему вычетов по модулю
пробегает приведенную систему вычетов по модулю  , то
, то 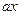 тоже пробегает приведенную систему вычетов по модулю
тоже пробегает приведенную систему вычетов по модулю  .
.
Доказательство. Действительно, чисел в системе будет 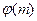 и они попарно не сравнимы по модулю
и они попарно не сравнимы по модулю  . Ибо, если
. Ибо, если 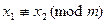 , а
, а 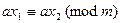 , то ввиду условия
, то ввиду условия 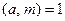 можно сократить обе части сравнения на общий множитель, что дает
можно сократить обе части сравнения на общий множитель, что дает 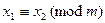 . Противоречие доказывает лемму.
. Противоречие доказывает лемму.
Теорема 13.8 (Эйлера).
Пусть 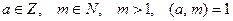 . Тогда
. Тогда 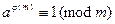 .
.
Доказательство. Пусть 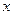 пробегает приведенную систему наименьших неотрицательных вычетов по модулю
пробегает приведенную систему наименьших неотрицательных вычетов по модулю  :
: 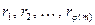 . Тогда в силу леммы 13.25
. Тогда в силу леммы 13.25 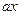 пробегает такую же систему
пробегает такую же систему 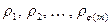 , но, вообще говоря, в ином порядке. Имеем
, но, вообще говоря, в ином порядке. Имеем
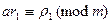 ,
,
 ,
,
. . . . . . . .
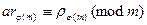 .
.
Перемножим почленно сравнения и находим
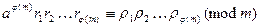 .
.
Теперь можно разделить обе части получившегося сравнения на общую величину 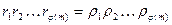 , что и дает утверждение теоремы:
, что и дает утверждение теоремы:
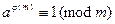 .
.
Следствие 1. Если  ,
, 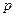 – простое число, то в условиях теоремы получаем, что
– простое число, то в условиях теоремы получаем, что
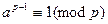 .
.
Этот результат называется малой теоремой Ферма.
Следствие 2. Избавляясь от условия взаимной простоты в формулировке, малую теорему Ферма можно записать в виде
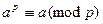 .
.
Это сравнение справедливо и при  .
.
Сравнения с неизвестным
Пусть задан многочлен 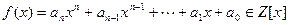 – многочлен с целыми коэффициентами и некоторое
– многочлен с целыми коэффициентами и некоторое 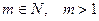 . Будем рассматривать уравнение
. Будем рассматривать уравнение
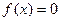 в кольце классов вычетов по модулю
в кольце классов вычетов по модулю  –
– 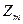 , соответствующим образом интерпретируя коэффициенты многочлена. Если прибегнуть к языку сравнений, то получим сравнение с неизвестным
, соответствующим образом интерпретируя коэффициенты многочлена. Если прибегнуть к языку сравнений, то получим сравнение с неизвестным
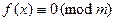 . (13.6)
. (13.6)
Определение 13.16. Степенью сравнения называется наибольший показатель степени буквы 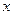 , при которой коэффициент не делится на модуль
, при которой коэффициент не делится на модуль  .
.
Дата добавления: 2019-07-26; просмотров: 704;
