АРИФМЕТИКА. Теория делимости 2 страница
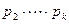
 .
.
И теперь уже 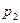 делит правую часть равенства. Повторяя рассуждение, приходим к выводу, что
делит правую часть равенства. Повторяя рассуждение, приходим к выводу, что 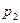 равно, например,
равно, например, 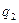 . И вновь сократим обе части равенства на общий множитель
. И вновь сократим обе части равенства на общий множитель 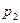 . Продолжая указанный процесс сокращения на общий множитель, видим, что
. Продолжая указанный процесс сокращения на общий множитель, видим, что 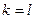 , ибо в противном случае, если
, ибо в противном случае, если 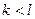 получили бы после очередного сокращения
получили бы после очередного сокращения
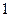
 ,
,
что невозможно. А если 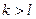 , то
, то 
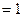 , что тоже невозможно. Это доказывает единственность разложения.
, что тоже невозможно. Это доказывает единственность разложения.
Следствие. Ввиду того, что в разложении (13.2) могут быть одинаковые сомножители, их можно собрать вместе и представить разложение в виде произведения степеней простых чисел, которое называется каноническим разложением числа  . Именно:
. Именно:
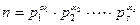 , где
, где 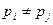 при
при 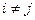 ,
, 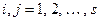 . (13.3)
. (13.3)
 Элементы теории непрерывных дробей
Элементы теории непрерывных дробей
Пусть 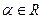 и через
и через 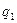 обозначим наибольшее целое число, не превосходящее
обозначим наибольшее целое число, не превосходящее 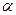 . Тогда при нецелом
. Тогда при нецелом 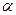 получим, что
получим, что  , где
, где 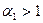 . Затем для
. Затем для  укажем число
укажем число 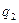 ближайшее к
ближайшее к  и не превосходящее его. Таким образом,
и не превосходящее его. Таким образом, 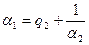 с
с 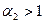 , что дает
, что дает 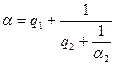
Продолжая этот процесс далее, получим для 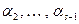
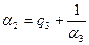 ,
,  ,
,
. . . . . . . . . .
 ,
, 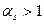 .
.
Это в итоге дает разложение числа 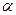 в непрерывную дробь:
в непрерывную дробь:


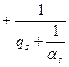 .
.
Если 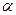 – число иррациональное, то и всякое
– число иррациональное, то и всякое  ,
, 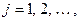 тоже будет иррациональным, поэтому в этом случае процесс разложения может быть продолжен неограниченно.
тоже будет иррациональным, поэтому в этом случае процесс разложения может быть продолжен неограниченно.
Если же 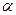 – рациональное, то оно может быть представлено несократимой обыкновенной дробью
– рациональное, то оно может быть представлено несократимой обыкновенной дробью 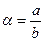 с положительным знаменателем, и указанный процесс оказывается конечным и может быть осуществлен с помощью алгоритма Евклида. Именно:
с положительным знаменателем, и указанный процесс оказывается конечным и может быть осуществлен с помощью алгоритма Евклида. Именно:
 ,
,  ,
,
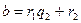 ,
, 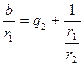 ,
,
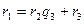 ,
, 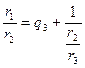 ,
,
. . . . . . . . . . . . . . . . . . .
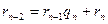 ,
, 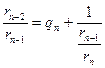 ,
,
 ,
, 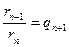 .
.
Это приводит к разложению
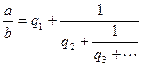

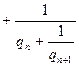 .
.
Числа 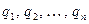 естественно называть неполными частными (в особенности это касается рационального случая). Дроби
естественно называть неполными частными (в особенности это касается рационального случая). Дроби
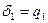 ,
, 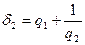 ,
, 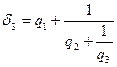 , . . .
, . . .
называются подходящими дробями. Они представляют собой приближения к разлагаемому числу. Представим способ описания подходящих дробей. Это сделать достаточно легко, если заметить, что при вычислении 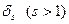 в выражении для
в выражении для  заменить число
заменить число 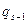 на число
на число 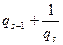 . Будем описывать подходящую дробь
. Будем описывать подходящую дробь 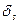
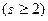 в виде
в виде 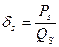 при этом полагая для единообразия
при этом полагая для единообразия 
 , а
, а  . Равенство
. Равенство 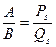 будем понимать как
будем понимать как 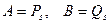 . Тогда имеем
. Тогда имеем
 ,
,
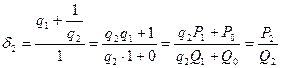 ,
,
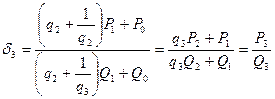 , . . .
, . . .
Далее, легко проверить индукцией, что
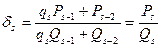 . (13.4)
. (13.4)
Значит, числители и знаменатели подходящих дробей для 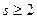 можно вычислять по рекуррентным формулам
можно вычислять по рекуррентным формулам
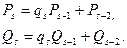 (13.5)
(13.5)
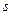
| . . . | 
| 
| ||||
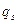
| 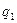
| 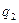
| 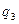
| . . . | 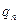
| 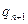
| |
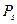
| 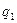
| 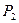
| 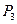
| . . . | 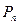
| 
| |

| 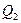
| 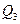
| . . . | 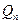
| 
|
Опишем схему вычисления для рационального случая.
Пример 13.2. Разложить в непрерывную дробь число 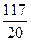 . Найдем неполные частные, применяя алгоритм Евклида. Имеем
. Найдем неполные частные, применяя алгоритм Евклида. Имеем
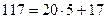 ,
,
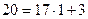 ,
,
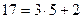 ,
,
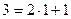 ,
,
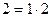 .
.
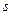
| ||||||
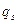
| ||||||
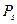
| ||||||

|
В итоге получаем разложение
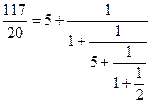 .
.
Для дальнейшего потребуется одно специальное свойство числителей и знаменателей подходящих дробей.
Лемма 13.8. При 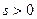 имеет место равенство
имеет место равенство
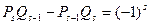 .
.
Доказательство. Обозначим левую часть соотношения через 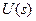 . Тогда при
. Тогда при 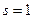 получим, что
получим, что 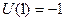 . Вычислим
. Вычислим 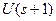 .
.
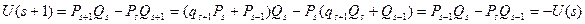 .
.
Таким образом, видно, что с изменением аргумента на единицу левая часть соотношения меняет знак. Теперь с учетом значения 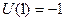 получаем требуемое.
получаем требуемое.
Пример 13.3. В завершение построим еще разложение в непрерывную дробь числа, являющегося квадратичной иррациональностью. Пусть 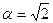 . Тогда имеем
. Тогда имеем
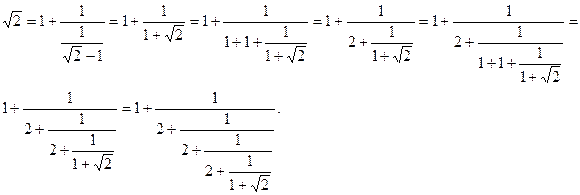
Понятно, что это разложение можно продолжать неограниченно долго.
Арифметические функции
Здесь рассмотрим некоторые специальные функции, широко используемые в арифметике.
Определение 13.7. Арифметической функцией называют отображение 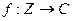 или
или 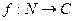 .
.
Пример 13.4. 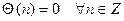 . Это функция тождественно равная нулю.
. Это функция тождественно равная нулю.
Пример 13.5. 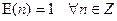 .
.
Пример 13.6 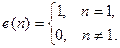
Пример 13.7. 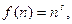 где
где 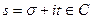 .
.
Пример 13.8. 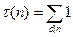 , здесь (и далее) суммирование распространено на все положительные делители числа
, здесь (и далее) суммирование распространено на все положительные делители числа 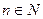 .
.
Определение 13.8. Арифметическая функция  называется мультипликативной, если она отлична от тождественного нуля (т.е., от
называется мультипликативной, если она отлична от тождественного нуля (т.е., от 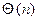 ) и выполняется условие:
) и выполняется условие:
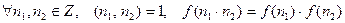 .
.
Множество мультипликативных функций обозначим через 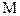 .
.
Пример 13.9.  .
.
Пример 13.10. 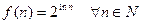 .
.
Пример 13.11. Функция 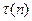 из примера 13.8.
из примера 13.8.
Определение 13.9. Мультипликативная функция  называется вполне мультипликативной, если
называется вполне мультипликативной, если
 .
.
Пример 13.12. Функция из примера 13.9.
Пример 13.13. Пусть 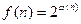 , где
, где  есть количество различных простых делителей
есть количество различных простых делителей  . Тогда
. Тогда  мультипликативна, но не вполне мультипликативна.
мультипликативна, но не вполне мультипликативна.
Пример 13.14. Для канонического разложения числа  ,
, 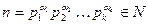 , определим арифметическую функцию
, определим арифметическую функцию 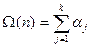 . Тогда
. Тогда 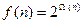 является вполне мультипликативной функцией.
является вполне мультипликативной функцией.
Рассмотрим некоторые свойства мультипликативных функций. Эти свойства представим в виде лемм.
Лемма 13.9. Пусть 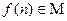 . Тогда
. Тогда 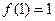 .
.
Доказательство. Так как  по определению не равна тождественному нулю, то пусть
по определению не равна тождественному нулю, то пусть  будет таким, что
будет таким, что 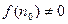 . Тогда имеем
. Тогда имеем
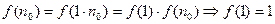 .
.
Лемма 13.10. Каждая мультипликативная функция вполне определяется своими значениями на степенях простых чисел.
Доказательство. Действительно, если 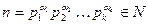 , то так как
, то так как 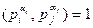 для
для 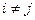 ,
, 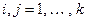 , то
, то 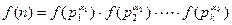 . С другой стороны, если заданы значения
. С другой стороны, если заданы значения  на степенях простых чисел, то определяется, ввиду канонического разложения, значение на любом натуральном
на степенях простых чисел, то определяется, ввиду канонического разложения, значение на любом натуральном  (случай
(случай 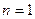 рассмотрен выше).
рассмотрен выше).
Лемма 13.11. Произведение нескольких мультипликативных функций есть снова функция мультипликативная.
Доказательство. Самостоятельно.
Лемма 13.12. Если 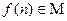 , то
, то  .
.
Доказательство. Пусть 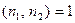 . Тогда
. Тогда
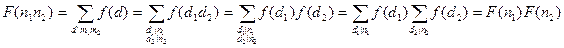 .
.
Лемма 13.13. Пусть 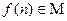 . Тогда для
. Тогда для 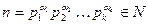
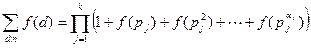 .
.
Доказательство следует из того, что произвольный делитель числа  имеет следующий вид:
имеет следующий вид:  , где
, где  ,
, 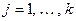 .
.
Пример 13.15. Рассмотрим функцию 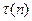 из примера 13.8. Тогда для
из примера 13.8. Тогда для 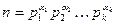 имеем:
имеем:
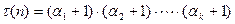 .
.
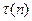 называется функцией делителей.
называется функцией делителей.
Определение 13.10. Функцией Мёбиуса 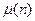 называется арифметическая функция, удовлетворяющая следующим условиям для
называется арифметическая функция, удовлетворяющая следующим условиям для 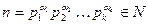 :
:
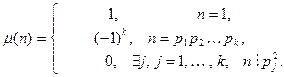
Лемма 13.14. 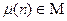 .
.
Доказательство. Ясно, что случай, когда 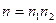 делится на квадрат простого числа, притом
делится на квадрат простого числа, притом 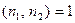 , тривиален. Поэтому рассмотрим вариант, когда
, тривиален. Поэтому рассмотрим вариант, когда 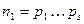 , а
, а 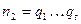 , где
, где 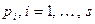 , и
, и 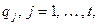 – простые попарно различные. Тогда
– простые попарно различные. Тогда
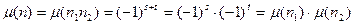 .
.
Лемма 13.15. Если 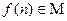 , то для
, то для 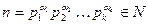 справедливо равенство
справедливо равенство
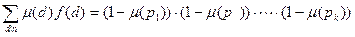 .
.
Доказательство. Тривиальное следствие определения и леммы 13.13.
Следствие 1. При 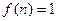 получаем
получаем
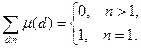
Следствие 2. При 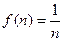 получаем
получаем
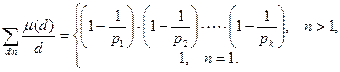
Теорема 13.5 (формула обращения Мёбиуса).
Пусть  – арифметическая функция. Тогда
– арифметическая функция. Тогда
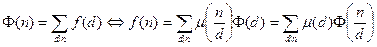 .
.
Доказательство. Необходимость.
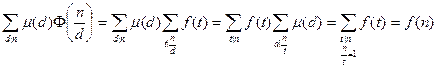 .
.
Здесь использовали следствие 1 из леммы 13.15.
Достаточность. Имеем
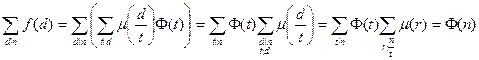 .
.
Здесь использовали то, что 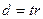 , значит,
, значит, 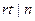 , т.е.,
, т.е., 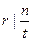 , и снова применили следствие 1 из леммы 13.15. Теорема доказана.
, и снова применили следствие 1 из леммы 13.15. Теорема доказана.
Наконец, приведем еще одну полезную лемму, использующую свойства функции Мёбиуса.
Лемма 13.16. Пусть натуральным  поставлены в соответствие любые вещественные или комплексные числа
поставлены в соответствие любые вещественные или комплексные числа 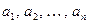 . Обозначим через
. Обозначим через  сумму значений
сумму значений  отвечающих значениям
отвечающих значениям  равным 1, а через
равным 1, а через 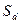 сумму значений
сумму значений  отвечающих значениям
отвечающих значениям  кратным
кратным 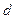 . Тогда
. Тогда
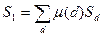 ,
,
где 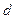 пробегает натуральные числа, делящие хотя бы одно значение
пробегает натуральные числа, делящие хотя бы одно значение 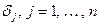 .
.
Доказательство. По лемме 13.15 имеем
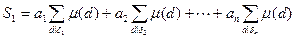 .
.
Теперь собирая вместе слагаемые с одним и тем же 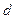 , вынося
, вынося 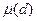 за скобки, получим требуемую сумму тех значений
за скобки, получим требуемую сумму тех значений  которые отвечают значениям
которые отвечают значениям  кратным
кратным 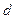 , а это и будут суммы
, а это и будут суммы 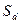 .
.
Определение 13.11. Функцией Эйлера 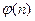 называется арифметическая функция, вычисляющая количество натуральных чисел в ряде
называется арифметическая функция, вычисляющая количество натуральных чисел в ряде 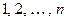 взаимно простых с
взаимно простых с  , иначе,
, иначе,

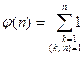 .
.
Исходя из определения, легко получить следующий результат.
Лемма 13.17. Если 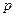 – простое число,
– простое число,  , то
, то
 ,
, 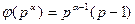 .
.
Новый результат получить несколько сложнее.
Лемма 13.18. 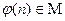 .
.
Доказательство. Применим лемму 13.16. Положим все 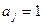 ,
, 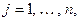 а в качестве
а в качестве 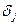 возьмем величины
возьмем величины 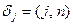 ,
,  . Тогда
. Тогда 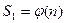 . По лемме имеем, что
. По лемме имеем, что 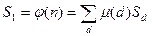 , где
, где 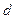 пробегает натуральные числа, делящие хотя бы одно значение
пробегает натуральные числа, делящие хотя бы одно значение 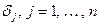 , т.е.,
, т.е.,  . Остается выяснить природу
. Остается выяснить природу 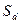 . Вновь по лемме это будет количество чисел вида
. Вновь по лемме это будет количество чисел вида 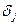 , кратных
, кратных 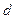 . Ясно, что это будут делители числа
. Ясно, что это будут делители числа  вида
вида 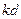 , где
, где 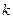 изменяется от 1 до
изменяется от 1 до 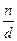 . Таким образом,
. Таким образом,  . Откуда получаем формулу
. Откуда получаем формулу
Дата добавления: 2019-07-26; просмотров: 729;
