АРИФМЕТИКА. Теория делимости 4 страница

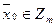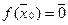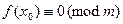Определение 13.17. Решением сравнения называется класс вычетов такой, что , или . Здесь .

Пример 13.17. Решением сравнения четвертой степени 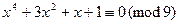является класс .

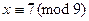Пример 13.18. Решением сравнения второй степени 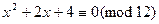являются классы 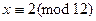и .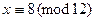

Любое сравнение теоретически можно решать перебором значений ПСВ по модулю . Но при больших это оказывается неудобным даже в простейших случаях.

Рассмотрим сравнения первой степени. Их в общем виде можно записать так:

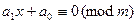, где 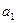не делится на .

Перепишем это сравнение, переобозначив коэффициенты,

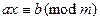. (13.7)

Пусть сначала 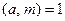. Заставим 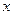пробегать ПСВ по модулю . В соответствии с леммой 13.23 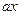тоже будет пробегать ПСВ модуля . Следовательно, для какого-то 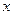, причем только одного, 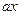попадет в класс, где находится число 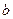, что и дает единственное решение в этом случае.

Пусть теперь 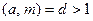. Тогда, если бы существовало решение 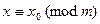, то выполнялось бы числовое сравнение 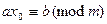, откуда понятно, что число 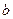должно делиться на 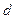. Так что, если 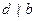, то решения заведомо нет. Пусть 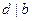. Тогда разделим обе части сравнения и модуль на 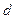. Положим, что 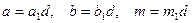. В этих обозначениях получаем новое сравнение

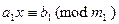, где уже .

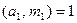Такое сравнение, как было показано, имеет и притом единственное решение 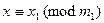, которое, очевидно, будет и решением исходного сравнения по модулю . Если теперь рассмотреть вычеты

,

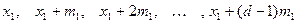то все они представляют одно решение по модулю 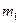, но являются разными решениями по модулю . Таким образом, в этом случае получаем 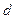решений по модулю . Это рассуждение приводит к теореме.

Теорема 13.9.

Сравнение первой степени 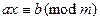, где 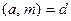, разрешимо тогда и только тогда, когда 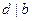. Если 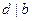, то сравнение имеет ровно 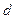решений.

Как уже было сказано, решения сравнения можно искать, перебирая какую-либо ПСВ по модулю . Но кроме этого имеется компактный способ описания решения. Пусть для определенности 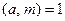. Тогда по теореме Эйлера 13.8

,

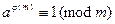откуда легко видеть, что класс 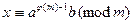будет решением сравнения (13.7) . Для получения такого решения явно требуется вычисление значения функции Эйлера, а это

далеко не простая задача. Поэтому приведем весьма эффективный метод решения, использующий разложение в непрерывную дробь числа 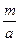, по-прежнему считая 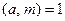. Из доказанного свойства непрерывных дробей (лемма 13.8) следует, что

.

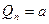В нашем случае, если – длина разложения, то , а . Поэтому имеем

.

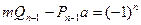Отсюда можно записать сравнение

.

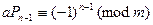Значит, ,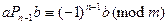

И тогда ,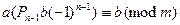

т.е., решением исходного сравнения будет класс 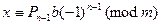. Вычисление числителя подходящей дроби может быть эффективно проведено, как показано выше.

Пример 13.19. Пусть надо решить сравнение 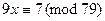. Разложим число 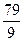в непрерывную дробь, точнее вычислим числители и знаменатели подходящих дробей:

,

,

,

.

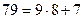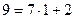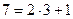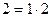Составим таблицу

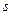
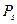
Теперь можно выписать решение: .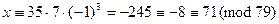

Если же пользовать компактным решением, то 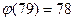, поэтому решение будет выглядеть так: .

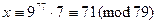Пример 13.20. Пусть надо решить сравнение 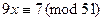. Легко видеть, не прибегая к алгоритму Евклида, что 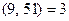и число 3 не делит число 7. Поэтому такое сравнение неразрешимо. Немного изменим его. Пусть требуется решить сравнение 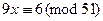. Разделим обе части сравнения и модуль на число 3, получим сравнение

.

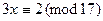Его легко решить перебором: 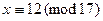. Тогда решениями исходного сравнения будут классы , , .

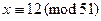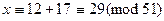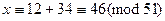Рассмотрим теперь системы сравнений первой степени следующего вида:

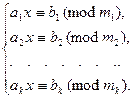(13.8) Решением такой системы естественно назвать класс по модулю наименьшего общего кратного 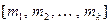, состоящий из чисел, удовлетворяющих каждому сравнению

системы. Если какое-либо сравнения не имеет решения, то вся система неразрешима. Такую систему можно решать последовательной подстановкой решений верхних сравнений в нижние.

Пример 13.21. Пусть требуется решить систему

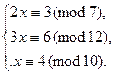
Решая первое сравнение, получим

, т.е., , .

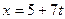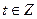Подставим этот результат во второе сравнение:

,

,

,

,

.

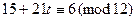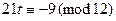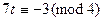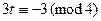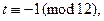
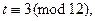
Откуда 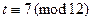, т.е.,

, , , .

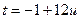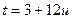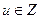Подставим эти результаты в выражение для х. Имеем

,

,

.

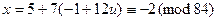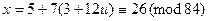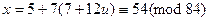Тогда , , .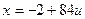

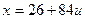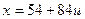Наконец, сделаем подстановку в третье сравнение каждого решения:

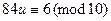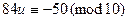, , , т.е.,

, , .

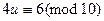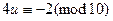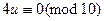Решаем эти сравнения

, , .

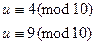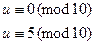Производя соответствующие подстановки в последние выражения для х , находим

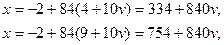
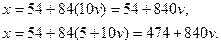
В итоге получили 6 решений системы по модулю 840, но по модулю 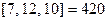их всего 3. Именно: , , .

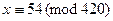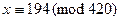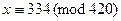Рассмотрим теперь случай взаимно простых модулей, причем будем считать, что все сравнения разрешены относительно х.

Теорема 13.10 (китайская теорема об остатках).

Пусть задана система сравнений

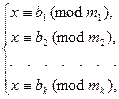
где 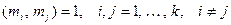. Тогда такая система разрешима и имеет единственное решение 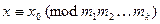. Здесь 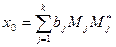, где

, , .

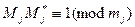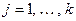Доказательство. Существование решения легко проверяется непосредственно. Остается показать единственность такого решения. Действительно, так как 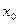удовлетворяет каждое сравнение системы, то можно получить систему эквивалентную исходной в виде

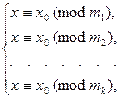
Откуда понятно, что любое другое решение обязано совпадать с приведенным в соответствии со свойствами числовых сравнений.

Пример 13.22. Решить систему

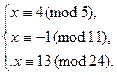
Найдем 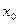. Для этого вычислим величины : , , .

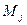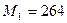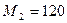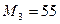Теперь вычислим 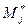, решив соответствующие сравнения:

, ;

, , ;

, , .

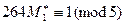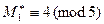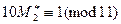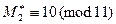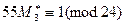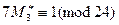Отсюда .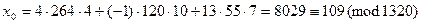

Теорема 13.11. Сравнение , где 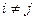, эквивалентно системе сравнений вида

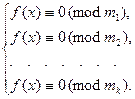
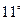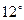Доказательство. Это прямое следствие свойств и числовых сравнений.

Следствие. Если 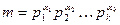, т.е., представлено в виде канонического разложения, то сравнение из теоремы равносильно системе

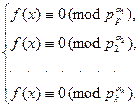
Таким образом, требуется уметь решать сравнения по модулю, равному степени простого числа. А последнее невозможно без умения решения сравнений по простому модулю. Метод перебора ПСВ здесь не учитывается.

Сравнения по простому модулю

Теорема 13.12. Пусть – простое число, 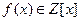, тогда сравнение 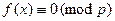эквивалентно сравнению степени не выше .

Доказательство. Разделим многочлен 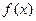на 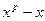с остатком, получим

,

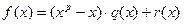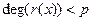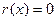где или . Но 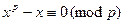, поэтому

,

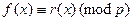что и требовалось.

Теорема 13.13. Пусть сравнение имеет более 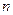решений. Тогда все коэффициенты многочлена в левой части делятся на .

Доказательство. Пусть сравнение имеет, например, 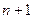решение. Обозначим вычеты этих решений через 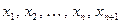. Представим многочлен из левой части сравнения в виде

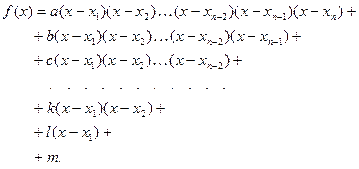
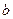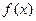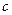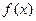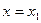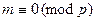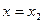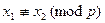Такое представление возможно, ибо, раскрывая произведения в правой части и представляя их в виде многочленов, коэффициент возьмем в виде разности коэффициентов при и первого многочлена, коэффициент – в виде разности коэффициентов при и первых двух многочленов и т.д. А затем положим и убедимся, что , после чего положим и получим, что , но , поэтому 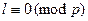. Продолжая этот процесс, убеждаемся что все коэффициенты 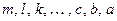кратны , но тогда и все коэффициенты исходного вида 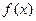– кратны как суммы чисел кратных .

Теорема 13.14 (критерий простоты Вильсона).

Натуральное число 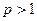является простым тогда и только тогда, когда выполнено условие

. (13.9)

Доказательство. Если 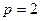, то результат очевиден. Пусть .

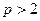Необходимость. Рассмотрим сравнение

.

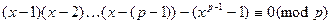Это сравнение имеет степень не выше 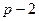, но при этом имеет не менее чем решение. Тогда по теореме 13.13 все коэффициенты многочлена, стоящего в левой части, должны быть кратны , и значит, свободный член, что и требовалось.

Достаточность. Докажем от противного. Пусть выполнено (13.9) , и – число составное, скажем 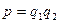, где 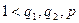. Тогда множитель 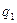обязательно встретится в произведении 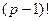, и так как 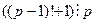и значит 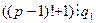, то свойству делимости должно быть 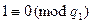, что невозможно. Противоречие доказывает достаточность.

Рассмотрение решения сравнений по модулю, равному степени простого числа, оставляем для дополнительного чтения учебной литературы.

Сравнения второй степени

В этом параграфе тоже ограничимся сравнениями по простому модулю. Последующие приложения в основном будут связаны с этим случаем, причем модуль предполагается нечетным. Само сравнений имеет вид:

.

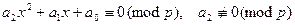Покажем, что это сравнение можно свести к двучленному случаю. Действительно, пусть сначала 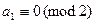. Тогда умножим обе части сравнения на , где 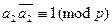. Получим

,

.

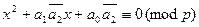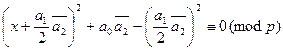Сделаем замену: 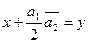и 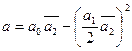. Тогда имеем сравнение вида

.

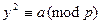Если же 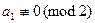, запишем исходное сравнение в виде

.

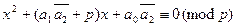Теперь коэффициент при 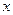снова четный, и можно повторить предыдущее рассуждение.

Таким образом, достаточно изучать указанные выше двучленные сравнения.

Определение 13.18. Пусть простое и 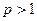. Целое 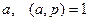называется квадратичным вычетом по модулю , если сравнение

13.10)

имеет решение. В противном случае 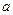называется квадратичным невычетом по этому модулю.

Лемма 13. 26. Если число 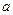является квадратичным вычетом, сравнение (13.10) имеет два решения.

Доказательство. Если решением сравнения является вычет 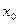, то очевидно, что 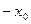тоже будет решением. Это второе решение отлично от первого, ибо, если 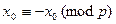, то 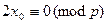. Но это невозможно, так как 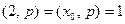. Более двух решений это сравнение иметь не может по теореме 13.13.

Лемма 13.27. Приведенная система вычетов по модулю содержит 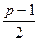квадратичных вычетов и 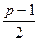квадратичных невычетов по модулю .