Среднее квадратическое отклонение
Дисперсия DX имеет размерность квадрата случайной величины X, что в сравнительных целях неудобно. Когда желательно, чтобы оценка разброса (рассеяния) имела размерность случайной величины, используют еще одну числовую характеристику - среднее квадратическое отклонение.
Средним квадратическим отклонением или стандартным отклонением случайной величины X называется квадратный корень из ее дисперсии, обозначают через 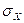 (или σХ, σ[Х], σ). Таким образом, по определению
(или σХ, σ[Х], σ). Таким образом, по определению
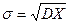 . .
| (5.18) |
Из свойств дисперсии вытекают соответствующие свойства среднего квадратического отклонения:
1. 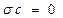 ,
,
2. 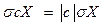 ,
,
3. 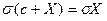 .
.
Для изучения свойств случайных явлений, независящих от выбора масштаба измерения и положения центра группирования, исходную случайную величину X приводят к некоторому стандартному виду: ее центрируют, т.е. записывают разность (X–MX) (геометрически означает, что начало координат переносится в точку с абсциссой, равной математическому ожиданию), затем делят на среднее квадратическое отклонение 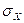 .
.
Случайную величину 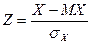 называют стандартной случайной величиной. Ее математическое ожидание равно 0, а дисперсия равна 1. Действительно,
называют стандартной случайной величиной. Ее математическое ожидание равно 0, а дисперсия равна 1. Действительно,
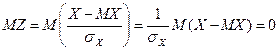 ,
,
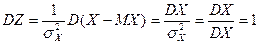 .
.
То есть Z – центрированная случайная величина, если MZ = 0,
Z – нормированная случайная величина, если DZ = 1.
Пример 5.4. Найти МХ, DX и 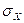 дискретной случайной величины Х, заданной рядом распределения:
дискретной случайной величины Х, заданной рядом распределения:
| Х | -1 | |||
| Р | 0,2 | 0,1 | 0,3 | 0,4 |
Решение:
Используя формулы (5.9), (5.13) и (5.18), находим:
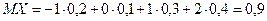 ,
,
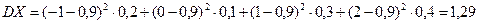 ,
,
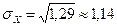 .
.
Дата добавления: 2017-03-29; просмотров: 319;
