Доверительный интервал для неизвестного математического ожидания a нормально распределенного признака с известным средним квадратическим отклонением находят по формуле
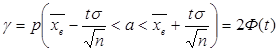
t – параметр, величину которого находят по таблицам Лапласа (см. приложение 3) из соотношения 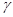 =2Φ(t).
=2Φ(t).
Приведенная формула позволяет решать следующие задачи:
1. По заданным надежности 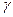 и объему выборки n находить точность
и объему выборки n находить точность 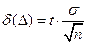 и доверительный интервал.
и доверительный интервал.
2. По заданным надежности 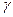 и точности δ находить объем выборки n.
и точности δ находить объем выборки n.
3. По заданным точности δ и объеме выборки n находить надежность 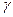 .
.
2. При определении доверительного интервала в случае нормального распределения при неизвестном σ признака X в генеральной совокупности применяют случайную величину
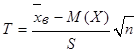 . ( n<30)
. ( n<30)
Эта величина соответствует закону t – распределения Стьюдента.
Дифференциальная функция распределения T обозначается S( 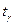 ; n) и зависит только от объема выборки n.
; n) и зависит только от объема выборки n.
Вероятность попадания случайной величины в соответствующий интервал равна
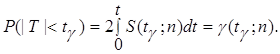
Доверительный интервал для оценки математического ожидания в этом случае находят по формуле

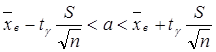
где 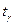 = t(
= t( 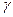 ; n) – числа, приведенные в специальных таблицах.
; n) – числа, приведенные в специальных таблицах.
Примечание. При большом объеме выборки (n ≥ 30) значения 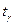 таблицы Стьюдента и t таблицы Лапласа практически равны. Поэтому выбор формулы, по которой определяют доверительный интервал, диктуется исходными данными
таблицы Стьюдента и t таблицы Лапласа практически равны. Поэтому выбор формулы, по которой определяют доверительный интервал, диктуется исходными данными
Пример. Для определения средней живой массы трехмесячного теленка определенной породы были взвешены 100 животных и результаты сведены в таблицу
| Масса, кг | 23-25 | 25-27 | 27-29 | 29-31 | 31-33 | 33-35 | 35-37 |
| Число телят, гол |
Найти:
1. Величины, которые следует принять за среднюю массу и среднее квадратическое отклонение.
2. Стандартную ошибку выборки и коэффициент вариации.
3. Доверительный интервал, который с вероятностью 0,95 заключает среднюю массу.
Решение:
1. В качестве приближенного значения средней массы принимаем выборочную среднюю, а за значение признака – середины интервалов
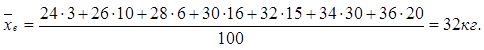
Вычисляем выборочную исправленную дисперсию
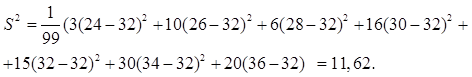
Находим исправленное выборочное среднее квадратичное отклонение
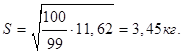
2. Стандартная ошибка выборки равна 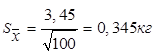
Коэффициент вариации
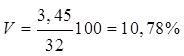
показывает, что изменчивость признака средняя.
3. Поскольку n = 100 > 30 и у нас случай нормального распределения, то доверительный интервал находим по формуле
Из условия 2Φ(t) = 0,95 определяем Φ(t) = 0,475,
а по таблице приложений находим t = 1,96.
Поэтому
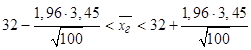
или 31,32 < 
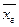 < 32,68 кг – доверительный интервал для заданной вероятности.
< 32,68 кг – доверительный интервал для заданной вероятности.
Объём выборки.Для определения n необходимо задать надежность (доверительную вероятность) оценки 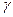 и точность (предельную ошибку выборки)
и точность (предельную ошибку выборки) 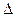 .
.
Объём выборки находят из формулы, выражающей предельную ошибку выборки через дисперсию признака. Например, для повторной выборки при оценке генеральной средней с надёжностью 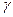 эта формула имеет вид:
эта формула имеет вид:
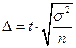 , откуда
, откуда 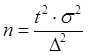 , где
, где 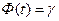
Необходимый объём выборки для получения достоверных результатов можно вычислить по формуле:
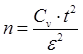
Как видно из формул, для определения обёма выборки необходимо знать характеристику генеральной совокупности 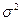 , которая не известна и для определения которой предполагается провести выборочное наблюдение. В качестве этой характеристики обычно используют выборочное данное
, которая не известна и для определения которой предполагается провести выборочное наблюдение. В качестве этой характеристики обычно используют выборочное данное 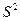 , т.е. полагают
, т.е. полагают 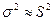
Дата добавления: 2017-02-20; просмотров: 675;
