Распределение Фишера.
Во многих задачах математической статистики, в особенности в дисперсионном анализе, важную роль играет распределение Фишера
(F-распределение), названное так по фамилии известного английского математика Р.А. Фишера (1925 г.)
Если U и V независимые случайные величины, распределенные по закону 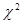 со степенями свободы
со степенями свободы 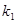 и
и 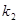 , то величина
, то величина
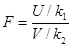 (*)
(*)
распределена по закону Фишера со степенями свободы 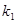 и
и 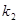 . Принимают, что U >V, так что переменная F принимает значения не меньшие 1.
. Принимают, что U >V, так что переменная F принимает значения не меньшие 1.
На практике часто применяется случайная величина
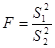
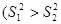 ), (**)
), (**)
Распределенная по закону Стьюдента с числом степеней свободы 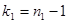 (для большей дисперсии) и
(для большей дисперсии) и 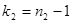 (для меньшей дисперсии). Здесь
(для меньшей дисперсии). Здесь
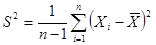 .
.
Покажем, что случайная величина (**) представляет собой частный случай случайной величины (*). Перепишем (**) в виде
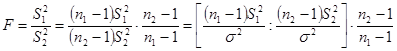 .
.
Случайные переменные 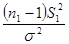 и
и 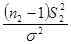 распределены по закону
распределены по закону 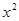 со степенями свободы
со степенями свободы 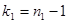 и
и 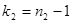 . Таким образом мы получили выражение (*).
. Таким образом мы получили выражение (*).
Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы 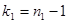 и
и 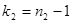 . Функция распределения величины F при небольшом объеме выборки n приближается к кривой нормального распределения.
. Функция распределения величины F при небольшом объеме выборки n приближается к кривой нормального распределения.
Наиболее часто функция F распределения табулирована для 5% (доверительная вероятность 0,95) и 1% (доверительная вероятность 0,99) уровней значимости и чисел степеней свободы 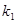 для большей дисперсии и
для большей дисперсии и 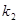 для меньшей дисперсии (см. приложение 2). На практике, в зависимости от поставленной задачи, при одном и том же значении доверительной вероятности используют распределение Фишера с односторонней (рис. 20) и двухсторонней (рис. 21) критическими областями. Для односторонней критической области по таблицам определяют критическое значение Fkp, соответствующее выбранному уровню значимости
для меньшей дисперсии (см. приложение 2). На практике, в зависимости от поставленной задачи, при одном и том же значении доверительной вероятности используют распределение Фишера с односторонней (рис. 20) и двухсторонней (рис. 21) критическими областями. Для односторонней критической области по таблицам определяют критическое значение Fkp, соответствующее выбранному уровню значимости 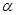 при степенях свободы
при степенях свободы 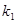 и
и 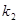 , для которого выполняется условие
, для которого выполняется условие 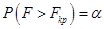 . В случае двухсторонней критической области критическим значением
. В случае двухсторонней критической области критическим значением 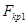 и
и 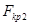 соответствует вероятности
соответствует вероятности 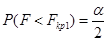 и
и 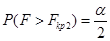 . На практике при двухсторонней критической области ограничиваются определением величины
. На практике при двухсторонней критической области ограничиваются определением величины 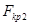 , для уровня значимости вдвое меньше заданного -
, для уровня значимости вдвое меньше заданного - 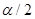 .
.

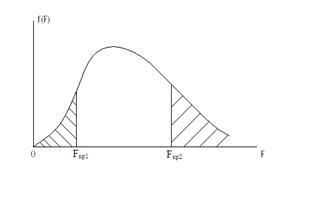
Рис. 20. Функция распределения Рис. 21. Функция распределения
Фишера с односторонней Фишера с двухсторонней
критической областью. критической областью.
Рассмотрим подробнее построение критических областей распределения Фишера. При использовании случайной величины F в качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий критическая область строится в зависимости от вида конкурирующей гипотезы.
Первый случай: Нулевая гипотеза 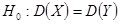 . Конкурирующая гипотеза
. Конкурирующая гипотеза 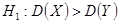 .
.
В этом случае строят одностороннюю, а именно правостороннюю, критическую область (рис. 20) исходя из требования, чтобы вероятность попадания величины F в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости р. Тогда правосторонняя критическая область определяется неравенством 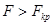 . Значение
. Значение 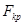 находят по заданному уровню значимости
находят по заданному уровню значимости 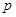 при степенях свободы
при степенях свободы 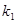 и
и 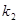 .
.
Второй случай: Нулевая гипотеза 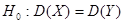 . Конкурирующая гипотеза
. Конкурирующая гипотеза 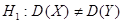 .
.
В этом случае строят двухстороннюю критическую область (рис.21) исходя из требования, чтобы вероятность попадания величины F в каждый из двух интервалов критической области, в предположении справедливости конкурирующей гипотезы, была равна 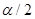 . Тогда критическая область определяется:
. Тогда критическая область определяется:  ,
, 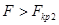 ; область принятия нулевой гипотезы:
; область принятия нулевой гипотезы: 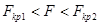 .
.
Дата добавления: 2017-02-20; просмотров: 2132;
