Геометрическое распределение
Дискретная случайная величина X имеет геометрическое распределение, если ее возможные значения: 1, 2, 3, 4, ..., а вероятности этих значений:
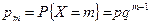 , ,
| (5.27) |
где 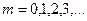
Геометрическое распределение имеет случайная величина X, равная числу опытов в схеме Бернулли, проведенной до первого успеха вероятность успеха р в единичном опыте.
Примерами реальных случайных величин, распределенных по геометрическому закону, являются: число выстрелов до первого попадания, число испытаний прибора до первого отказа, число бросаний монеты до первого выпадения цифры и т.д.
Ряд распределения случайной величины X, имеющей геометрическое распределение, имеет вид
| X = m | … | |||
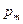
| р | 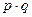
| 
| … |
Контроль: 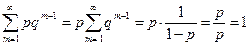 .
.
Вероятности 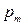 образуют геометрическую прогрессию р,
образуют геометрическую прогрессию р, 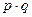 ,
,  ,…. По этой причине распределение (5.27) называют геометрическим.
,…. По этой причине распределение (5.27) называют геометрическим.
Найдем математическое ожидание и дисперсию геометрического распределения. Производящей функцией для случайной величины Х является функция
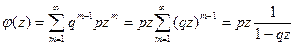 ,
,
т.е. 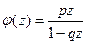 . Для нее
. Для нее 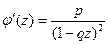 ,
, 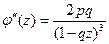 .
.
Следовательно,
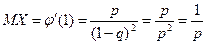 , ,
 , ,
| (5.28) |
т.е.
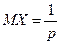 ,
, 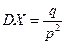 и значит
и значит 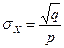 .
.
Пример 5.8.Вероятность попадания в цель при отдельном выстреле для данного стрелка равна 0,1. Найти математическое ожидание и дисперсию случайной величины Х – числа выстрелов по цели до первого попадания.
Решение:
Случайная величина Х имеет геометрическое распределение с параметром 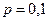 . По формулам (5.28):
. По формулам (5.28):
 ,
,
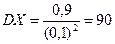 ,
,
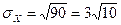 .
.
Дата добавления: 2017-03-29; просмотров: 393;
