Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы записи комплексного числа
Поскольку комплексное число мы определили как упорядоченную пару действительных чисел, то вполне естественно изобразить комплексное число 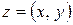 точкой плоскости с декартовыми координатами
точкой плоскости с декартовыми координатами 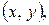 либо вектором, идущим из начала координат в эту точку (рис. 1).
либо вектором, идущим из начала координат в эту точку (рис. 1).
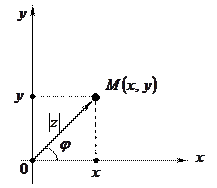 |
Рис. 1.
На оси Ох расположены все действительные числа, а на оси Оу – чисто мнимые, т.е. комплексные числа вида 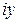 .
.
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью (её также обозначают C). Ось абсцисс называется действительной осью, а ось ординат – мнимой.
Длина вектора 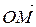 , изображающего комплексное число
, изображающего комплексное число 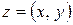 , есть модуль комплексного числа:
, есть модуль комплексного числа:
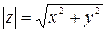 ,
,
а угол 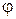 , который образует этот вектор с осью Ох, называется аргументом комплексного числа
, который образует этот вектор с осью Ох, называется аргументом комплексного числа 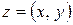 .
.
Очевидно, что угол 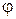 определён с точностью до
определён с точностью до 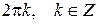 .
.
Условимся называть главным значением аргумента – значение угла 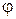 в интервале
в интервале 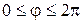 . Символически главное значение аргумента комплексного числа обозначают:
. Символически главное значение аргумента комплексного числа обозначают: 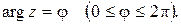
Тогда всю совокупность значений аргумента 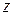 обозначают символом:
обозначают символом:
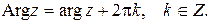
Очевидны формулы:
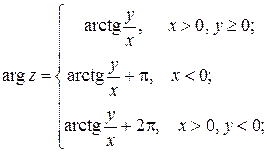
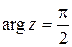 при
при 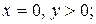
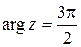 при
при 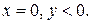
Из рис. 1 легко получить соотношения: 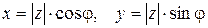 , тогда
, тогда
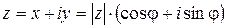 .
.
Определение. Представление комплексного числа 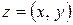 в виде
в виде 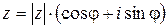 называется тригонометрической формой записи комплексного числа.
называется тригонометрической формой записи комплексного числа.
Для сокращения записи комплексных чисел в тригонометрической форме удобно использовать формулу Эйлера:
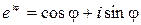 .
.
Тогда комплексное число можно записать в виде:
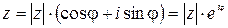 .
.
Определение. Представление комплексного числа 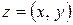 в виде
в виде 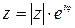 называется показательной формой записи комплексного числа.
называется показательной формой записи комплексного числа.
Таким образом, комплексное число 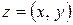 может быть записано в трёх равноправных формах:
может быть записано в трёх равноправных формах:
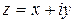 – алгебраическая форма записи комплексного числа;
– алгебраическая форма записи комплексного числа;
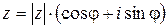 – тригонометрическая форма записи комплексного числа;
– тригонометрическая форма записи комплексного числа;
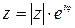 – показательная форма записи комплексного числа,
– показательная форма записи комплексного числа,
где 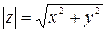 ,
, 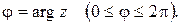
Пример 3.Записать комплексные числа в трёх формах записи:
а) 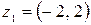 ; б)
; б) 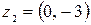 ; б)
; б) 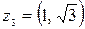 и изобразить их векторами на плоскости.
и изобразить их векторами на плоскости.
Решение.а) 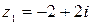 – алгебраическая форма записи комплексного числа
– алгебраическая форма записи комплексного числа 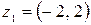 . Находим модуль и аргумент комплексного числа
. Находим модуль и аргумент комплексного числа 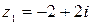 .
.
Здесь 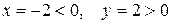 ,
, 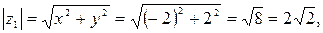
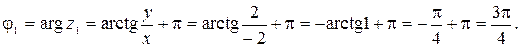 Значит,
Значит,
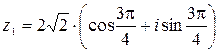 – тригонометрическая форма записи комплексного числа
– тригонометрическая форма записи комплексного числа 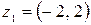 ;
;
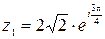 – показательная форма записи комплексного числа
– показательная форма записи комплексного числа 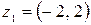 .
.
б) 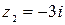 – алгебраическая форма записи комплексного числа
– алгебраическая форма записи комплексного числа 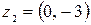 . Находим модуль и аргумент комплексного числа
. Находим модуль и аргумент комплексного числа 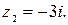 Здесь
Здесь 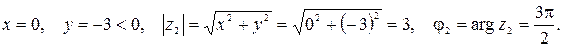 Значит,
Значит,
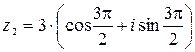 – тригонометрическая форма записи комплексного числа
– тригонометрическая форма записи комплексного числа 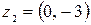 ;
;
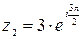 – показательная форма записи комплексного числа
– показательная форма записи комплексного числа 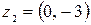 .
.
в) 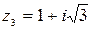 – алгебраическая форма записи комплексного числа
– алгебраическая форма записи комплексного числа 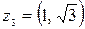 . Находим модуль и аргумент комплексного числа
. Находим модуль и аргумент комплексного числа 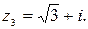 Здесь
Здесь
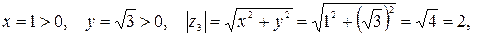
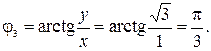 Значит,
Значит,
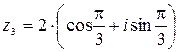 – тригонометрическая форма записи комплексного числа
– тригонометрическая форма записи комплексного числа 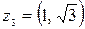 ;
;
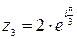 – показательная форма записи комплексного числа
– показательная форма записи комплексного числа 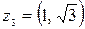 .
.
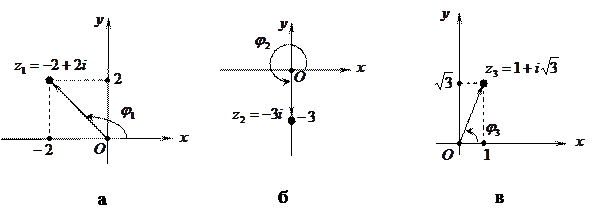 |
Рис. 2.
Изображения комплексных чисел представлены на рис. 2.
4.3. Формула Муавра и извлечение корня п-ой степени из комплексного числа
Вычислив произведение комплексных чисел, записанных в тригонометрической форме, можно убедиться, что модуль и аргумент комплексного числа обладают следующими свойствами:
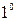 . Модуль произведения комплексных чисел равен произведению модулей этих чисел:
. Модуль произведения комплексных чисел равен произведению модулей этих чисел: 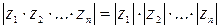 .
.
 . Аргумент произведения комплексных чисел равен сумме аргументов этих чисел:
. Аргумент произведения комплексных чисел равен сумме аргументов этих чисел: 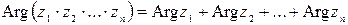 .
.
Используя эти свойства, легко можно получить формулу возведения комплексного числа в целую положительную степень, а именно:
если 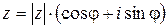 , то
, то
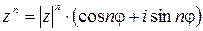 – формула Муавра,
– формула Муавра,
или в показательной форме записи:
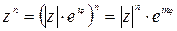 .
.
Определение.Корнем п-ой степени из комплексного числа 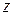 называется такое комплексное число
называется такое комплексное число 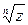 , которое, будучи возведено в степень п даст число
, которое, будучи возведено в степень п даст число 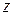 .
.
Из определения и формулы Муавра ясно, что модуль искомого корня будет 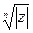 , а аргумент
, а аргумент 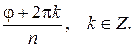
Таким образом,
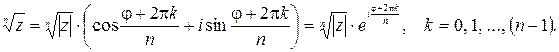 (1)
(1)
Придавать 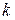 значения, большие
значения, большие 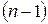 , не имеет смысла, так как будем получать уже имеющиеся значения аргумента (с точностью до
, не имеет смысла, так как будем получать уже имеющиеся значения аргумента (с точностью до 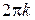 ).
).
Следовательно, корень п-ой степени из комплексного числа 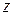 имеет п различных значений, модули которых одинаковы (
имеет п различных значений, модули которых одинаковы ( 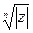 ), т.е. все значения корня лежат на окружности с центром в начале координат радиуса
), т.е. все значения корня лежат на окружности с центром в начале координат радиуса 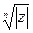 , а аргументы последовательных значений отличаются на угол
, а аргументы последовательных значений отличаются на угол 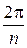 .
.
Пример 4.Используя формулу Муавра, вычислить:
а) 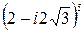 ; б)
; б) 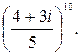
Решение.а) Представим число 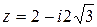 в тригонометрической форме. Имеем:
в тригонометрической форме. Имеем: 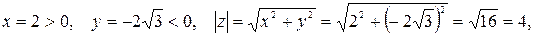
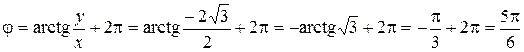 . Значит,
. Значит,
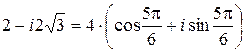 – тригонометрическая форма записи комплексного числа
– тригонометрическая форма записи комплексного числа 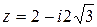 .
.
Применяя формулу Муавра, получим:
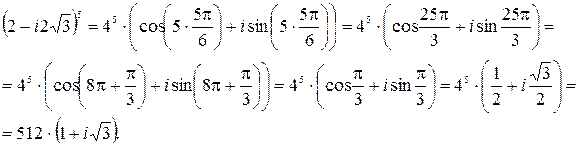
б) Представим число 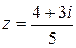 в тригонометрической форме. Имеем:
в тригонометрической форме. Имеем: 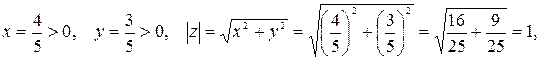
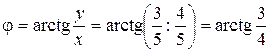 . Поэтому
. Поэтому
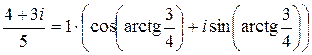 – тригонометрическая форма записи комплексного числа
– тригонометрическая форма записи комплексного числа 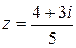 .
.
Применяя формулу Муавра, получим:
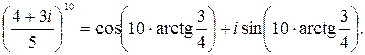
Пример 5.Найти все значения корня: 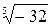 .
.
Решение.Представим комплексное число 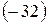 в тригонометрической форме. Здесь
в тригонометрической форме. Здесь 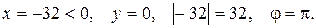 Поэтому
Поэтому
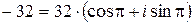 .
.
По формуле (1) находим:
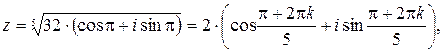 где
где 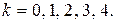
Полагая 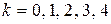 , получим:
, получим:
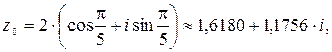
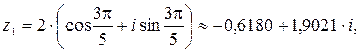

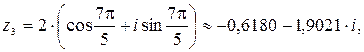
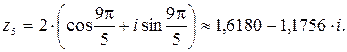
Найденным корням соответствуют вершины правильного пятиугольника, вписанного в окружность радиуса 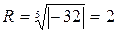 с центром в начале координат (рис. 3).
с центром в начале координат (рис. 3).
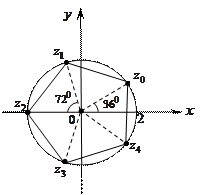 |
Рис. 3.
Дата добавления: 2017-04-20; просмотров: 1984;
