Гипергеометрический закон распределения

Дискретная случайная величина X имеет гипергеометрическое распределение, если она принимает значения 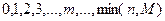с вероятностями

,

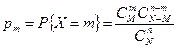(5.29)

где 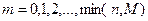, М ≤ N, m ≤ n, n ≤ N; n, М, N - натуральные числа.

Гипергеометрическое распределение возникает в случаях, подобных следующему: в урне N шаров, из них М белых, а остальные черные. Вынимается n шаров. Требуется найти вероятность того, что среди извлеченных шаров будет ровно m белых (остальные черные). Случайная величина X - число белых шаров среди извлеченных из урны.

Математические ожидания дискретной случайной величины X, имеющей гипергеометрическое распределение, есть

,

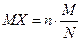(5.30)

а ее дисперсия

.

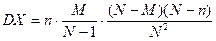(5.31)

Гипергеометрическое распределение определяется тремя параметрами N, М, n. Если n мало по сравнению с N (практически 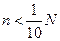), он приближается к биномиальному распределению с параметрами n и :

.

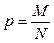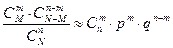Гипергеометрическое распределение используется при решении задач, связанных с контролем качества продукции и т.п.

Пример 5.9. В группе из 21 студентов 5 девушек. Из этой группы наудачу отбираются 3 студента. Составить закон распределения дискретной случайной величины Х – числа девушек из отобранных студентов. Найти МХ.

Решение:

Случайная величина Х принимает значения 0, 1, 2, 3. Вероятности этих значений находим по формуле (5.29):

,

,

,

.

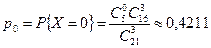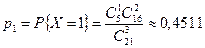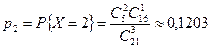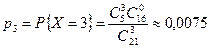Ряд распределения:

X = m
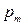
	0,4211	0,4511	0,1203	0,0075

Значение МХ найдем двумя способами:

а) по ряду распределения:

;

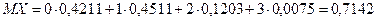б) по формуле (5.30)

.

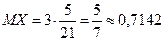Равномерный закон распределения

Непрерывная случайная величина X имеет равномерное распределение на отрезке [а, b], если ее плотность вероятности f(x) постоянна на этом отрезке, а вне его равна нулю:

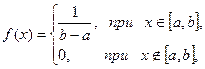
(5.32)

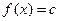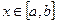т.е. при , но

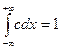
отсюда следует, что 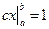, 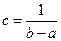. Вместо отрезка [а, b] можно писать (а, b) или (а, b], [а, b), так как случайная величина X - непрерывна.

График плотности 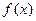для равномерного распределения непрерывной случайной величины Х изображен на рис. 5.8.

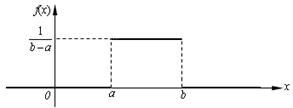
Рис. 5.8.

Равномерное распределение случайной величины X на участке [а, b] (или (а, b)) будем обозначать: X ~ R[а, b].

Найдем функцию распределения 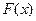для X ~ R[а, b]. Учитывая, что

,

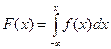имеем

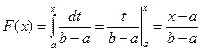, при ;

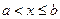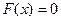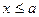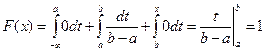, при ,

, при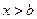

Таким образом,

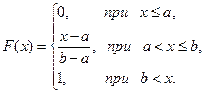
(5.33)

График 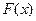изображен на рис. 5.9.

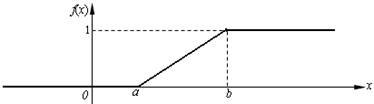
Рис. 5.9.

Определим МХ и DX случайной величины X ~ R[а, b].

.

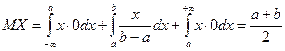Математическое ожидание случайной величины X ~ R[a, b] равно абсциссе середины отрезка: МХ совпадает с медианой, т.е. .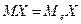

.

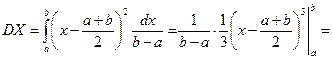
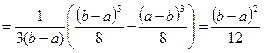Таким образом, для непрерывной случайной величины X ~ R[а, b] имеем

, .

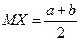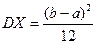(5.34)

К случайным величинам, имеющим равномерное распределение, относятся: время ожидания пассажиром транспорта, курсирующего с определенным интервалом; ошибка округления числа до целого (она равномерно распределена на отрезке [-0,5; 0,5]. И вообще случайные величины, о которых известно, что все ее значения лежат внутри некоторого интервала и все они имеют одинаковую вероятность (плотность).

Дискретная случайная величина Х имеет равномерное распределение, если она принимает целочисленные значения 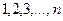с вероятностью 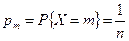, где .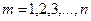

В этом случае , .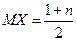

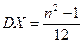Пример 5.10. Пусть случайная величина Х ~ R(a, b). Найти вероятность попадания случайной величины Х в интервал (a, b), принадлежащий целиком интервалу (a, b).

Решение:

Согласно свойству 2 плотности 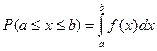, имеем:

,

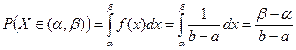т.е. 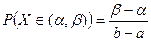. Геометрически эта вероятность представляет собой площадь прямоугольника (рис. 5.10, закрашенная область):

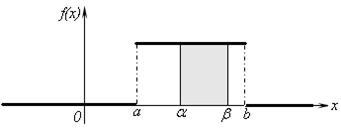
Рис. 5.10.