I. Нормальные законы распределения.

Появление погрешностей при проведении измерения - событие случайное, поэтому величины погрешности характеризуют вероятностными параметрами. Основной из них - закон распределения параметра (случайной величины) по интервалу измерений. Измеряют напряжение, ток, дискретными параметрами.

Характеристики же однотипны. Наиболее распространенными законами распределения считают:

1. Нормальный закон распределения.

2. Равномерный (равновероятностный) закон распределения.

3. Треугольный (Симпсона) закон распределения.

4. Колоколообразный.

5. Закон распределения Релея.

6. Косинусный закон (или arccos).

Нормальный закон распределения применяется наиболее часто, поскольку более ярко отражает случайные свойства величины.

Xi-DX

Xизм = X ± DX

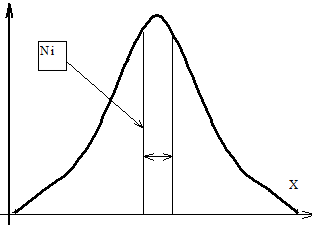
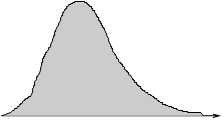
Поскольку Хизм можно представить через сумму среднего (истинного) значения X и погрешности измерения, то графически выборку определенного числа измерений k можно представить обобщенным графиком, на котором ордината Ni показывает число (количество) измеренных значений с величиной (X± DX) . Выборка дает какое-то произвольное распределение. Для большинства распределения по краям убывают. Поэтому принято описывать, присваивать реальным распределениям различные законы. Наиболее часто используется нормальный закон. На графике можно представить количество измеренных величин, попадающих в определенный интервал. С уменьшением гистограмма по форме стремится к математическому представлению закона распределения. На гистограмме по ординате частость, т.е. количество опытов с одинаковыми результатами. Кривая, описывающая закон распределения - пронормированная величина. Каждое ее значение разделено на число выборок (опытов). Поэтому площадь под кривой равна интегралу.

N P(X)

S=1

Х Х

Для конкретных Для любого числа

числов опытов опытов

Погрешности стремятся описать тем или иным законом. Нормальный закон используют, поскольку основное влияние оказывают на результат измерения случайная составляющая погрешности и систематическая. Первая и обеспечивает разброс в доверительном интервале, систематическая же составляющая показывает сдвиг полученного среднего значения относительно номинальной величины. Поскольку по опытным данным можно определить, что систематическая составляющая присутствует, ее возможно скомпенсировать. Случайную же составляющую погрешностей не исключить. Поэтому случайная составляющая оказывает большее влияние на разброс результата.

Нормальный закон распределения используют, если причины, определяющие погрешность при измерениях независимы - некоррелированы и их несколько.

Основные свойства нормального распределения: