Нормальный закон распределения
Нормальный закон («закон Гаусса») играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Нормальный закон наиболее часто встречается на практике.
Непрерывная случайная величина Х распределена по нормальному закону с параметрами а и 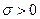 , если ее плотность распределения имеет вид
, если ее плотность распределения имеет вид
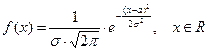 . .
| (5.38) |
Тот факт, что случайная величина Х имеет нормальное распределение с параметрами а и σ сокращенно записывается так: X ~ N(а, σ).
Функция распределения непрерывной случайной величины X ~ N(а, σ) имеет вид
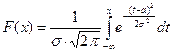 . .
| (5.39) |
Если а = 0 и σ = 1, то нормальное распределение с такими параметрами называется стандартным. Плотность стандартной случайной величины имеет вид
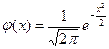 . .
| (5.40) |
Функция распределения случайной величины X ~ N(0, 1) имеет вид
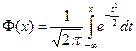 . .
| (5.41) |
и называется функцией Лапласа. Она связана с нормированной функцией Лапласа 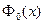 равенством
равенством
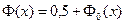 . .
| (5.42) |
Математическое ожидание случайной величины X ~ N(а, σ) имеет вид: 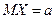 , ее дисперсия
, ее дисперсия 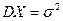 , где σ – среднее квадратичное отклонение.
, где σ – среднее квадратичное отклонение.
Для случайной величины X ~ N(а, σ):
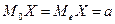 ,
, 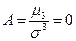 ,
, 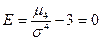 .
.
Исследуем дифференциальную функцию (5.38) нормального закона:
1. 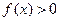 при любом
при любом 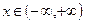 ; график функции расположен выше оси Ох.
; график функции расположен выше оси Ох.
2. Ось Ох служит асимптотой графика функции 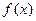 , так как
, так как 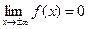 .
.
3. Функция 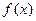 имеет один максимум при x=а, равный
имеет один максимум при x=а, равный 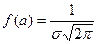 .
.
4. График функции 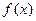 симметричен относительно прямой x=а, так как аналитическое выражение
симметричен относительно прямой x=а, так как аналитическое выражение 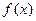 содержит разность x - а в квадрате.
содержит разность x - а в квадрате.
5. Можно убедиться, что точки 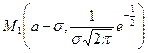 и
и 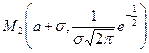 , являются точками перегиба графика функции
, являются точками перегиба графика функции 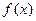 .
.
Пользуясь результатами исследования, строим график плотности распределения вероятности нормального закона - кривую распределения, называемую нормальной кривой, или кривой Гаусса (рис. 5.13).
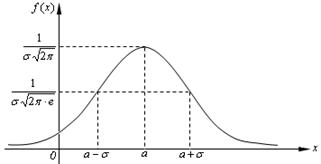
Рис. 5.13.
Вероятность попадания случайной величины X ~ N(а, σ) на заданный участок 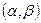 равна
равна
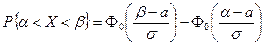 . .
| (5.43) |
Через функцию Лапласа 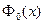 выражается и функция распределения
выражается и функция распределения 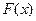 нормально распределенной случайной величины Х:
нормально распределенной случайной величины Х:
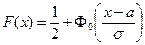 . .
| (5.44) |
Если функция Лапласа есть
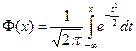 ,
,
то с учетом (5.42) и (5.44) получим
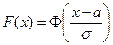 . .
| (5.45) |
Равенство (5.43) можно переписать в виде:
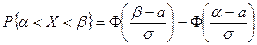 . .
| (5.46) |
На практике часто приходится вычислять вероятность попадания нормально распределенной случайной величины в интервал, симметричный относительно центра рассеяния а. Пусть таким интервалом будет 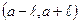 длины
длины 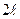 . Тогда
. Тогда
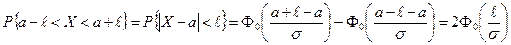
т.е.
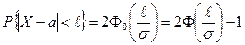 . .
| (5.47) |
В равенстве (5.47) полагая 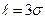 , получим
, получим 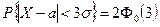 . По таблице значений для
. По таблице значений для 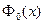 находим:
находим: 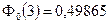 . Следовательно,
. Следовательно, 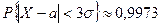 , т.е. отклонение случайной величины Х от своего математического ожидания меньше, чем
, т.е. отклонение случайной величины Х от своего математического ожидания меньше, чем 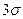 - почти достоверное событие.
- почти достоверное событие.
Практически достоверно, что случайная величина X ~ N(а, σ) принимает свои значения в промежутке 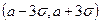 . Это утверждение называется «правилом трех сигм».
. Это утверждение называется «правилом трех сигм».
Пример 5.12. При измерении детали получаются случайные ошибки, подчиненные нормальному закону распределения с параметром 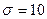 мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.
мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.
Решение:
По формуле (5.47) находим:
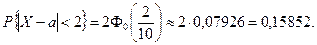
Вероятность того, что эта ошибка превышает 2 мм в одном измерении, равна
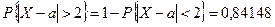 .
.
По теореме умножения вероятность того, что во всех трех опытах ошибка измерения превышает 2 мм, равна 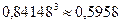 . Следовательно, искомая вероятность равна
. Следовательно, искомая вероятность равна 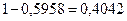 .
.
Дата добавления: 2017-03-29; просмотров: 288;
