Показательный закон распределения
Непрерывная случайная величина X имеет показательный (или экспоненциальный) закон распределения, если ее плотность вероятности имеет вид
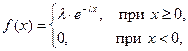
| (5.35) |
где 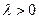 - параметр распределения.
- параметр распределения.
График плотности 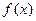 приведен на рис. 5.11.
приведен на рис. 5.11.
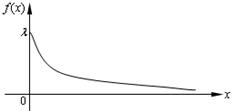
Рис. 5.11.
Функция распределения показательного закона имеет вид:
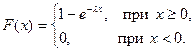
| (5.36) |
График 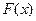 представлен на рис. 5.12.
представлен на рис. 5.12.
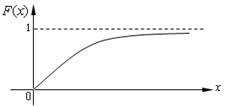
Рис. 5.12.
Математическое ожидание и дисперсия показательного распределения имеют вид:
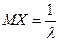 , , 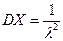 , , 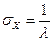 . .
| (5.37) |
Вероятность попадания случайной величины Х, распределенной по показательному закону, в интервал 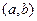 равна:
равна:
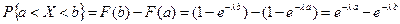 .
.
Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания, в физике, в теории надежности, а также для описания распределения случайной величины вида: длительность работы прибора до первого отказа, длительность времени обслуживания в системе массового обслуживания и т.д.
Рассмотрим, непрерывную случайную величину Т - длительность безотказной работы прибора. Функция распределения случайной величины Т, т.е. 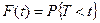 , определяет вероятность отказа за время длительностью t. И, значит, вероятность безотказной работы за время t равна
, определяет вероятность отказа за время длительностью t. И, значит, вероятность безотказной работы за время t равна
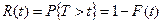 .
.
Функция R(t) называется функцией надежности.
Случайная величина Т часто имеет показательное распределение. Ее функция распределения имеет вид
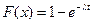 .
.
В этом случае функция надежности имеет вид
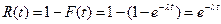 ,
,
т.е.
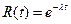 R(t) e-λt,
R(t) e-λt,
где λ - интенсивность отказов, т.е. среднее число отказов в единицу времени.
Показательный закон - единственный из законов распределения, который обладает свойством «отсутствия последствия» (т.е. если промежуток времени Т уже длился некоторое время τ, то показательный закон распределения остается таким же и для оставшейся части 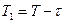 промежутка).
промежутка).
Пример 5.11. Случайная величина Т – время работы радиолампы имеет показательное распределение. Найти вероятность работы того, что лампа проработает не менее 800 часов, если среднее время работы радиолампы 400 часов.
Решение:
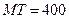 , значит по формуле (5.37),
, значит по формуле (5.37),
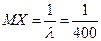 .
.
Искомая вероятность
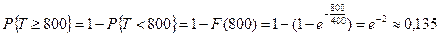 .
.
Дата добавления: 2017-03-29; просмотров: 408;
